Valeur moyenne

Valeur moyenne - Valeur efficace

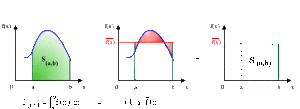
On appelle valeur moyenne d'une fonction \(f(x)\) définie et continue sur l'intervalle \([a, b],\) l'expression :

\(\boxed{\overline{f}(x)=\frac1{b-a}\int_a^b f(x)dx}\)

Exemple : Valeur moyenne d'une fonction f(x)

Calculer la valeur moyenne de la fonction \(f(x) = x^3\) sur l'intervalle \([-1 , 3] .\)

Par définition : \(\overline{f}(x)=\frac1{b-a}\int _a^bf(x)dx\)

D'où \(\color{red}\boxed{\color{black}\overline{f}(x)}\color{black}=\frac{1}{3-(-1)}\int_{-1}^3x^3dx=\frac14[\frac{x^4}{4}]_{-1}^3=\frac1{16}(81-1)=\color{red}\boxed{\color{black}5}\)

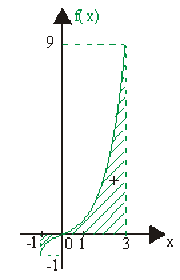
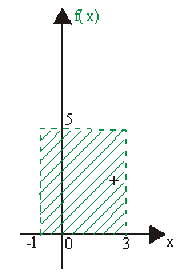
\(\color{red}\boxed{\color{black}\int_{-1}^3x^3dx=4\times \overline{f}(x)=20~u.a.}\)

Si une fonction \(f(t)\) est périodique de période \(T,\) la valeur moyenne s'exprime par :

\(\boxed{\color{red}\overline{f}(t)=\frac 1T\int_0^Tf(t)dt}\)

Exemple : Valeur moyenne d'une fonction périodique

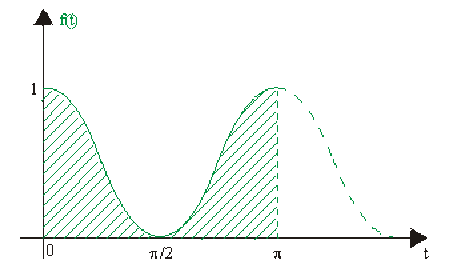
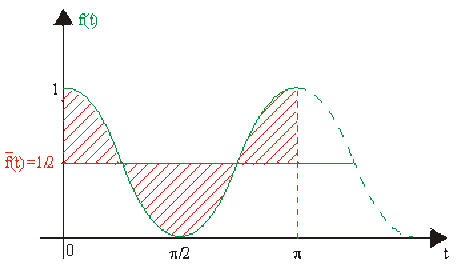
Calculer la valeur moyenne, sur une période, de la fonction \(f(t) = \cos^2 t\)

Par définition : \(\overline{f}(t)=\frac1T\int_0^Tf(t)dt~~(\text{ou }\frac1T\int_a^{a+T}f(t)dt)\)

or \(f(t)\) est une période \(T=\pi\) car \(\cos^2t=\frac{1+\cos2t}2\)

D'où \(\color{red}\boxed{\color{black}\overline{f}(x)}\color{black}=\frac1{\pi}\int_0^{\pi}\cos^2tdt=\frac{1}{\pi}\int_0^{\pi}\frac{1+\cos2t}2dt\\=\frac1{2\pi}[\int_0^{\pi}dt+\int_0^{\pi}\cos2tdt]=\frac1{2\pi}[t+\frac{\sin2t}2]_0^{\pi}=\color{red}\boxed{\color{black}\frac12}\)

\(\color{red}\boxed{\color{black}\int_0^T\cos^2tdt=T\times\overline{f}(x)=\frac{\pi}2~u.a.}\)

La valeur moyenne \(\overline{f}(x)\)apparaît donc comme la hauteur d'un rectangle de base \((a -b )\) ayant le même axe que celle limitée par la courbe représentative de \(f(x),\) l'axe \(Ox\) et les droites verticales d'équations \(x = a\) et \(x = b.\)

Définition : Valeur efficace

On appelle valeur efficace \(F\) de la fonction \(f(x),\) la racine carrée de la valeur moyenne du carré de \(f(x).\)

\(\boxed{F=\sqrt{\overline{f^2}(x)}=\sqrt{\frac1{b-a}\int_a^bf^2(x)dx}}\)

Si une fonction \(f(t)\) est périodique de période \(T,\) la valeur efficace est :

\(\boxed{\color{red}F=\sqrt{\frac1T\int_0^Tf(t)^2dt}}\)

Exemple : Valeur efficace d'une fonction f(x)

Calculer la valeur efficace de la fonction \(f(x) = 1/x\) sur l'intervalle \([1 , 4]\)

Par déffinition : \(F=\sqrt{\overline{f^2}(x)}=\sqrt{\frac1{b-a}\int_a^bf^2(x)dx}\)

or \(\frac1{b-a}\int_a^bf^2(x)dx=\frac1{4-1}\int_1^4\frac1{x^2}dx=\frac13[\frac{-1}{x}]_1^4=\frac{-1}3[\frac14-1]=\frac14\)

d'où \(\color{red}\boxed{\color{black}F}\color{black}=\sqrt{\frac14=\color{red}\boxed{\color{black}0.5}}\)

NB. La valeur moyenne étant \(\color{red}\boxed{\color{black}\overline{f}(x)}\color{black}=\frac13\int_1^4\frac1xdx=\frac13[\ln x]_1^4=\frac23\ln2~~\# \color{red}\boxed{\color{black}0.46}\)