Calculs de longueurs
En coordonnées cartésiennes
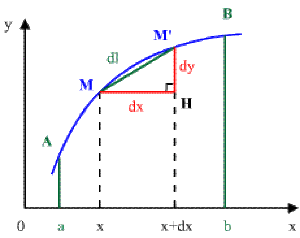
La longueur \(AB,\) de l'arc de courbe est décomposée en segments élémentaires de longueur \(dl.\)
Dans le triangle \(MHM',\) on a :
\(\widehat{MM'}\approx MM'=\sqrt{\overline{MH}^2+\overline{HM'}^2}\)
\((dl)^2=(dx)^2+(dy)^2\\=(1+(\frac{dy}{dx})^2)(dx)^2\\dl=\sqrt{1+y'^2}dx\)
\(\boxed{l_{\widehat{AB}}=\int_a^b\sqrt{1+y'^2}dx}\)
Exemple : Longueur d'une chaînette
Calcul de la longueur de la chaînette d'équation \(y=\cosh(x)=\frac{e^x+e^{-x}}{2}\) comprise entre les points \(A(0,1)\) et \(B(1,\cosh(1)).\)
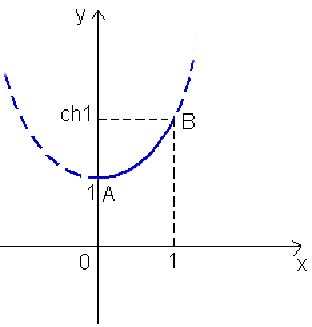
Par définition, en coordonnées cartésiennes: \(dl=\sqrt{1+y'^2}dx\)
d'où \(\color{red}l\color{black}=\int_{x=0}^{x=1}\sqrt{1+\sinh^2(x)}dx=\int_{x=0}^{x=1}\cosh xdx\\=[\sinh(x)]_0^1=\color{red}\sinh(1)=\frac{e^1-e^{-1}}{2}\approx1,18ul\)
En coordonnées paramétriques
Quand la courbe est représentée sous forme paramétrique, le calcul du segment élémentaire \(dl\) s'exprime par :
\(\begin{array}{l l}x(t)=f(t)&dx=f'(t)dt\\y(t)=g(t)&dy=g'(t)dt\end{array}\)
\(dl=\sqrt{(dx)2+(dy)^2}=\sqrt{f'^2(t)+g'^2(t)}dt\)
\(\boxed{l_{\widehat{AB}}=\int_{t_1}^{t_2}\sqrt{f'^2(t)+g'^2(t)}dt}\)
Exemple : Longueur d'une arche de cycloïde
Déterminer la longueur de l'arche de la cycloïde d'équations paramétriques : \(\begin{cases}x(t)=R(t-\sin t)\\y(t)=R(1-\cos t)\end{cases}\)
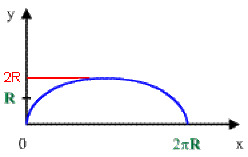
Une arche est décrite lorsque \(t\) varie de \(0\) à \(2\pi,\)
or \(\begin{cases}x'(t)=R(1-\cos t)\\y'(t)=+R\sin t\end{cases}.\)
d'où \(x'^2(t)+y'^2(t)=R^2[(1-\cos t)^2+\sin^2t]\)
\(=R^2[1-2\cos t+\cos^2 t+\sin^2t]\)
\(=2R^2(1-\cos t)\)
\(=4R^2\sin^2\frac t2\)
La longueur de l'arche de la cycloïde devient :
\(l=\int_0^{2\pi}\sqrt{x'^2(t)+y'^2(t)}dt=\int_0^{2\pi}2R\sin\frac t2dt=-4R[\cos\frac{t}{2}]_0^{2\pi}\)
donc \(\color{red}l\color{black} = - 4R [ \cos\pi - \cos0 ] =\color{red} 8R\)
En coordonnées polaires
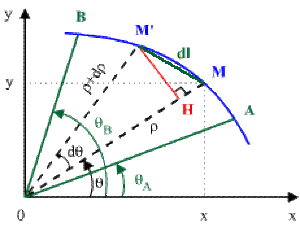
Comme précédemment, la longueur \(dl\) de l'arc élémentaire est définie par :
\(\widehat{MM'}\approx MM'=\sqrt{\overline{MH}^2+\overline{HM'}^2}\)
\((dl)^2=(dx)^2+(dy)^2\)
Après transformation en coordonnées polaires, nous obtenons :
\(\begin{array}{l l}x=\rho\cos\theta&dx=\cos\theta d\rho-\rho\sin\theta d\theta\\y=\rho\sin\theta&dy=\sin\theta d\rho+\rho\cos\theta d\theta\end{array}\)
\((dl)^2=(dx)^2+(dy)^2=(d\rho)^2+(\rho d\theta)^2\)
\(dl=\sqrt{(d\rho)^2+(\rho d \theta)^2}\\=\sqrt{\rho^2+(\frac{d\rho}{d\theta})^2}d\theta\)
pour \(\rho = f (\theta)\)
\(\boxed{l_{\widehat{AB}}=\int_{\theta_A}^{\theta_B}\sqrt{\rho^2+\rho'^2}d\theta}\)
Exemple : Longueur de la cardioïde
Calcul de la longueur de la cardioïde d'équation \(\rho=a(1+\cos\theta)\)
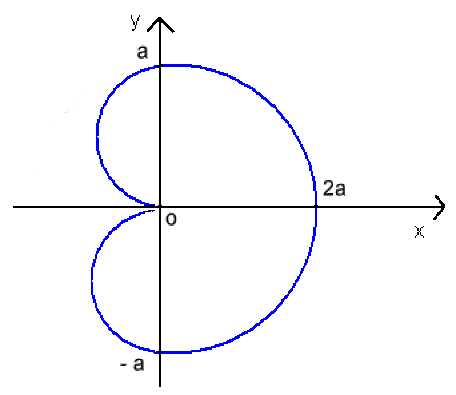
Par définition, en coordonnées polaires : \(l=2\int_{\theta=0}^{\theta=\pi}\sqrt{\rho^2+\rho'^2}d\theta\)
Pour des raisons de symétries, la longueur totale de la cardioïde sera: \(l=2\int_{\theta=0}^{\theta=\pi}\sqrt{\rho^2+\rho'^2}d\theta\)
avec \(\rho^2+\rho'^2=a^2(1+\cos\theta)^2+(-a\sin\theta)^2\)
\(=2a^2(1+\cos\theta)=4a^2\cos^2\frac{\theta}2\)
d'où \(l=2\times2a\int_{\theta=0}^{\theta=\pi}\cos\frac{\theta}2d\theta=4a\times2[\sin\frac{\theta}2]_0^{\pi}\)
\(\color{red}l = 8a\)