Calculs d'aires
Aires planes
En coordonnées cartésiennes
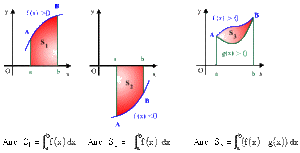
La surface comprise entre la courbe représentative de \(f(x),\) l'axe des abscisses \(Ox\) et les droites verticales d'équations \(x = a\) et \(x = b\) est calculée par :
\(\boxed{S=\int_a^bf(x)dx}\)
Suivant les valeurs de \(f(x)\) sur \([a, b],\) nous calculerons l'aire (grandeur physique positive) par les expressions suivantes :
Exemple : Aire délimitée par une chaînette et une droite
Déterminer l'aire délimitée par les courbes \(y_1^2 = 9x\) et \(y_2 = 3x.\)
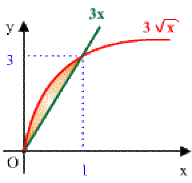
Par définition, l'aire colorée est :
\(A=\int_0^1[y_1(x)-y_2(x)]dx\)
\(=\int_0^1[3\sqrt x-3x]dx=[3\frac{2x^{3/2}}3 - \frac32x^2]_0^1\)
\(=[2x^{3/2}-\frac 32 x^2]_0^1=2-\frac32\)
\(\color{red}A=\frac12\)
En coordonnées paramétriques
On applique toujours la relation \(S=\int_a^bydx\)dans le cas où \(\begin{cases}x(t)=f(t)\\y(t)=g(t)\end{cases}\)avec \(dx = f '(t) dt ,\) et :
\(\boxed{S=\int_{t_1}^{t_2}g(t)f'(t)dt}\)
Exemple : Aire plane d'une arche de cycloïde
Déterminer l'aire comprise entre l'axe des abscisses \(Ox\) et l'arche de la cycloïde d'équations :
\(x(t)=R(t-\sin t)\) et \(y(t)=R(1-\cos t)\)
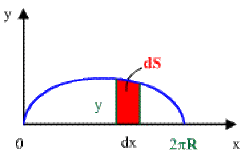
On prend comme élément d'aire : \(dA = y dx\)
les bornes d'intégration étant \(t_1 = 0\) et \(t_2 = 2\pi.\)
d'où
\(S=\int_0^{2\pi R}ydx=\int_0^{2\pi}R(1-\cos t)R(1-\cos t)dt\\=R^2\int_0^{2\pi}(1-\cos t)^2dt\\=R^2\int_0^{2\pi}(1-2\cos t+\cos^2 t) dt\\=R^2\int_0^{2\pi}(1-2\cos t+\frac{1+\cos2t}2)dt\\=R^2[\frac32t-2\sin t+\frac{\sin 2t}4]_0^{2\pi}\\\color{red}A=3\pi R^2\)
En coordonnées polaires
La courbe en coordonnées polaires étant notée \(\rho = f(\theta),\) on prend pour surface élémentaire \(dS,\) l'aire du triangle \(OMM'\) et vaut :
\(dS=\frac12\rho(\rho d\theta)=\frac12\rho^2d\theta\Rightarrow\color{red}S=\frac12\int_{\theta_A}^{\theta_B}\rho^2d\theta\)
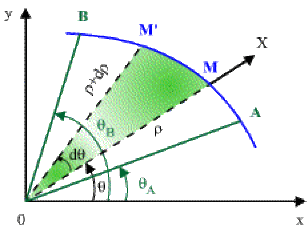
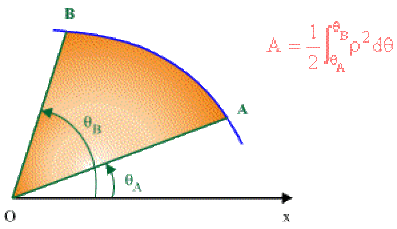
1er cas : Aire d'un secteur dont le sommet est le pôle \(O.\)
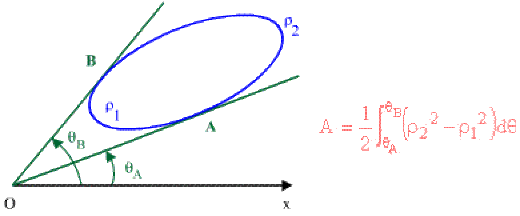
2ème cas : Aire d'une courbe fermée ne comprenant pas le pôle \(O.\)
3ème cas : Aire d'une courbe fermée comprenant le pôle \(O.\)
Exemple : Aire plane intérieure à la lemniscate de Bernoulli
Calcul de l'aire intérieure à la lemniscate de Bernoulli d'équation polaire :
\(r^2=a^2\cos2q\)
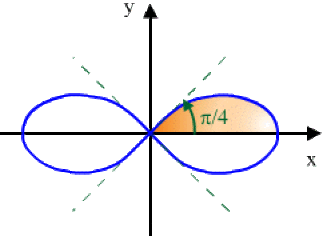
D'après la symétrie de la courbe, l'aire est quatre fois celle de l'aire colorée.
\(A=4[\frac12\int_{\theta_1}^{\theta_2}\rho^2d\theta]=2\int_0^{\pi/4}a^2\cos 2 \theta d\theta\)
\(\color{red}\boxed{A}\color{black}=2a^2[\frac{\sin2\theta}2]_0^{\pi/4}=\color{red}\boxed{a^2}\)
Exemple : Aire plane delimitée par deux courbes
Calcul de l'aire hachurée de la boucle de lemniscate de Bernoulli d'équation \(\rho_2^2=4\cos2\theta,\) exterieure au cercle d'équation polaire \(\rho_1=\frac{2\sqrt6}3\cos\theta\)
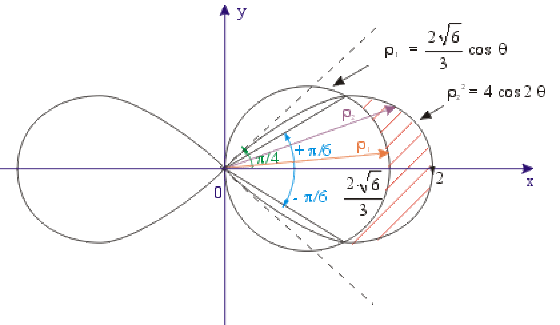
Aux points d'intersection \(M_1\) et \(M_2\) nous avons:
\(\rho_1=\rho_2\Rightarrow4\cos2\theta=\frac{24}9\cos^2\theta\Leftrightarrow\\2\cos^2\theta-1=\frac23\cos^2\theta\Leftrightarrow\\\cos^2\theta=\cos\theta=\pm\frac{\sqrt3}2\)
d'où les solutions:
\(\cos\theta_1=-\frac{\sqrt3}2\Leftrightarrow\theta_1=-\frac{\pi}6[2\pi]\\\cos\theta_2=+\frac{\sqrt3}2\Leftrightarrow\theta_2=+\frac{\pi}{6}[2\pi]\)
Par définition l'aire hachurée s'exprime par:
\(A=\frac12\int_{\theta_1}^{\theta_2}(\rho_2^2-\rho_1^2)d\theta=\frac 12\int_{\theta_1=-\frac{\pi}6}^{\theta_2=+\frac{\pi}6}4(\cos2\theta-\frac23\cos^2\theta)d\theta\\=2\int_{\theta_1=-\frac{\pi}6}^{\theta_2=+\frac{\pi}6}[\cos2\theta-\frac23(\frac{1+\cos2\theta}2)]d\theta\\=\frac23\int_{\theta_1=-\frac{\pi}6}^{\theta_2=+\frac{\pi}6}(2\cos2\theta-1)d\theta=\frac23[\sin2\theta - \theta]_{-\frac{\pi}6}^{+\frac{\pi}6}\\\color{red}A\color{black}=\frac43(\sin\frac{\pi}3-\frac{\pi}6)=\frac{4}{3}(\frac{\sqrt3}2-\frac{\pi}6)=\color{red}\frac29(3\sqrt3-\pi)\approx0,46~~ua\)
Exemple : Aire plane de la cardioïde
Calcul de l'aire plane intérieure à la cardioïde d'équation polaire :
\(\rho = a(1+\cos\theta)\)
D'après la définition:
\(A=\frac12\int_0^{2\pi}\rho^2d\theta=\frac12a^2\int_0^{2\pi}(1+\cos\theta)^2d\theta\\=\frac{a^2}2\int_0^{2\pi}(1+2\cos\theta+\cos^2\theta)d\theta\\=\frac{a^2}2\int_0^{2\pi}(\frac32+2\cos\theta+\frac{\cos2\theta}2)d\theta\\=\frac{a^2}2[\frac32\theta+2\sin\theta+\frac14\sin2\theta]_0^{2\pi}\\\boxed{\color{red}A=\frac32\pi a^2}\)
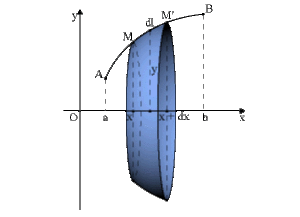
Aires des surfaces de révolution
Une surface de révolution est engendrée par la rotation d'une courbe autour d'un axe \(Ox,\) ou axe polaire par exemple. L'aire élémentaire \(dS = 2\pi ydl\) ainsi balayée par l'arc \(\widehat{MM'}\)(ou par la corde \(MM')\) est celle d'un tronc de cône et définie en fonction du système de coordonnées.
En coordonnées cartésiennes
L'élément de longueur est donné par \(dl=\sqrt{1+y'^2}dx\)d'où la surface de révolution de \(y(x)\) en rotation autour de l'axe \(Ox\) :
\(\color{red}S\color{black}=\int_a^b2\pi ydl=\color{red}\int_{x_1}^{x_2}2\pi y\sqrt{1+y'^2}dx\)
Exemple : Aire de la surface de révolution d'un arc de la chaînette
Calcul de l'aire de la surface (appelée cathénoïde) engendrée par la rotation de l'arc de la chaînette \(y = \cosh x,\) autour de l'axe \(Ox\) compris entre les points d'abscisses \(x= 0\) et \(x = 1\)
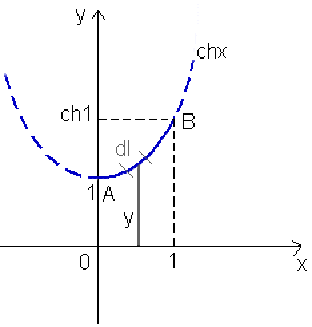
Par définition: \(dS=2\pi ydl\)
avec \(dl=\sqrt{1+y'^2}dx\)
d'où \(S=\int_{x_1=0}^{x_2=1}2\pi y\sqrt{1+y'^2}dx=2\pi\int_0^1\cosh x\sqrt{1+\sinh^2x}dx\\S=2\pi\int_0^1\cosh^2xdx=2\pi\int_0^1\frac{1+\cosh2x}2dx\\S=\pi[\int_0^1dx+\int_0^1\cosh2xdx]\)
\(\color{red}S\color{black}=\pi[1+\frac{\sinh2x}2]_0^1=\pi[1+\frac{\sinh2}2]=\color{red}\frac{\pi}4(4+e^2-e^{-2})\approx8,84~~u.a.\)
En coordonnées paramétriques
L'élément de longueur est donné par: \(dl=\sqrt{f'^2(t)+g'^2(t)}\)d'où la surface de révolution de la courbe définie paramétriquement par :
\(\begin{cases}x(t)=f(t)\\y(t)=g(t)\end{cases}\)en rotation autour de l'axe \(Ox.\)
\(\color{red}S\color{black}=\int_a^b2\pi ydl=\color{red}\int_{t_1}^{t_2}2\pi g(t)\sqrt{f'^2(t)+g'^2(t)}dt\)
Exemple : Aire de la surface de révolution de l'arche de la cycloïde
Calcul de l'aire de la surface de révolution engendrée par la rotation de l'arche de la cycloïde autour de l'axe des abscisses.
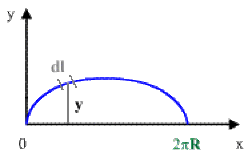
Par définition: \(dS = 2\pi y dl\)
avec \(dl=\sqrt{f'^2(t)+g'^2(t)}dt\)
Les expressions paramétriques des coordonnées de la cycloïde étant:
\(x = f(t) = R(t-\sin t)\)
\(y = g(t) = R(1-\cos t)\)
Nous aurons: \(S=\int_{t_1=0}^{t_2=2\pi}2\pi g(t)\sqrt{f'^2(t)+g'^2(t)}dt\)
or \(f'^2(t)+g'^2(t)=R^2(1-\cos t)^2+R^2\sin^2t=2R^2(1-\cos t)=4R^2\sin^2\frac t2\)
donc \(S=\int_{t_1=0}^{t_2=2\pi}2\pi R(1-\cos t)(2R\sin\frac t2)dt=8\pi R^2\int_{t_1=0}^{t_2=2\pi}\sin^3\frac t2 dt\)
D'après la relation de linéarisation: \(\sin^3t=\frac14(3\sin t-\sin 3t)\)
nous en déduisons: \(\color{red}S\color{black}=8\pi R^2\times\frac14\int_{t_1=0}^{t_2=2\pi}(3\sin\frac t2-\sin\frac{3t}2)dt\\=-2\pi R^2[6\cos \frac t2-\frac 23\cos\frac{3t}2]_0^{2\pi}\\=-2\pi R^2(-12+\frac43)=\color{red}\frac{64}3R^2\)
En coordonnées polaires
L'élément de longueur est donné par : \(dl=\sqrt{\rho^2+\rho'^2}d\theta\)d'où la surface de révolution de la courbe en rotation autour de l'axe polaire:
\(\color{red}dl\color{black}=\int_a^b2\pi ydl=\color{red}\int_{\theta_1}^{\theta_2}2\pi \rho\sin\theta\sqrt{\rho^2+\rho'^2}d\theta\)
d'où l'aire totale balayée par l'arc de courbe \(AB\) :
\(\boxed{\color{red}S=\int_a^b2\pi y\sqrt{1+y'^2}dx}\)
Exemple : Aire de la surface de révolution de la cardioïde
Calcul de l'aire de la surface engendrée par la rotation de la cardioïde d'équation \(\rho=a(1+\cos\theta)\) autour de l'axe polaire.
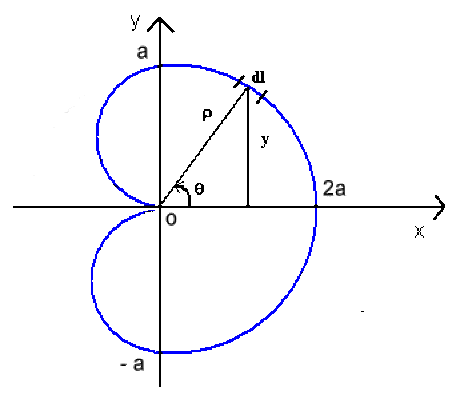
Par définition: \(dS=2\pi ydl\)
avec \(dl=\sqrt{\rho^2+(\frac{d\rho}{d\theta})^2}d\theta=\sqrt{\rho^2+\rho'^2}d\theta\)
et \(y=\rho\sin\theta\)
L'équation polaire de la cardioïde étant : \(\rho=a(1+\cos\theta)\)
nous en déduisons: \(\rho'=-a\sin\theta\)
d'où:
\(\color{red}S\color{black}=\int_0^{\pi}2\pi ydl=\int_0^{\pi}2\pi\rho\sin\theta\sqrt{a^2(1+\cos\theta)^2+a^2\sin^2\theta}d\theta\\=2\pi\int_0^{\pi}a^2(1+\cos\theta)\sin\theta\sqrt{2(1+\cos\theta)}d\theta\\=2\pi a^2\int_0^{\pi}(1+\cos\theta)\sin\theta\sqrt{4\cos^2\frac{\theta}2}d\theta\\=4\pi a^2\int_0^{\pi}(1+\cos\theta)\sin\theta\cos\frac{\theta}2d\theta\\=16\pi a^2\int_0^{\pi}\cos^4\frac{\theta}2\sin\frac{\theta}2d\theta\\=\frac{-32\pi a^2}5[\cos^5\frac{\theta}2]_0^{\pi}=\color{red}\frac{32}5\pi a^2\)