Calculs de volumes
En général le calcul des volumes nécessite l'emploi des intégrales triples, mais des formes à géométrie simple ou de révolution permettent l'utilisation d'une intégrale simple.
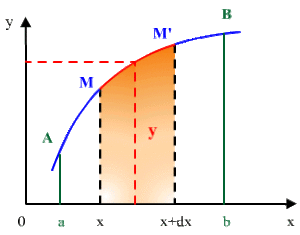
Le volume élémentaire \(dV\) engendré par l'aire hachurée lors de la rotation autour de l'axe \(Ox\) est donc :
\(dV = \pi y^2 dx\)
d'où le volume engendré par l'aire délimitée par l'arc \(AB,\) l'axe \(Ox\) et les droites d'équations \(x = a\) et \(x = b\) sera :
\(\boxed{\color{red}V=\int_a^b\pi y^2dx}\)
Exemple : Volume de la sphère
Déterminer le volume de la sphère.
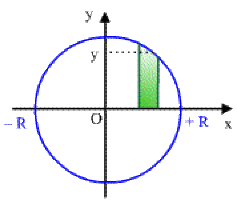
\(V=\int_{-R}^{+R}\pi y^2dx=2\int_0^{-R}\pi y^2dx\)
or comme \(y=\sqrt{R^2-x^2},\) il vient :
\(V=2\pi\int_0^R(R^2-x^2)dx=2\pi[R^2x-\frac{x^3}3]_0^R\\=2\pi[R^3-\frac{R^3}3]\\\color{red}V=\frac{4\pi R^3}3\)