Question 1
Durée : 5 mn
Note maximale : 4
Question
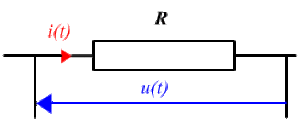
Un circuit électrique est parcouru par un courant alternatif sinusoïdal : \(i(t) = I_m \sin w t\) (période \(T = 2\pi / \omega).\)
La différence de potentiel aux bornes d'un dipôle (résistor de résistance de \(R)\) est de la forme : \(u(t) = U_m \sin (\omega t + \varphi)\) où \(I_m,\) \(U_m\) et \(\varphi\) sont des constantes.
Déterminer la valeur moyenne de \(i(t)\) sur une alternance (demi - période).
Solution
La valeur moyenne \(\overline{f(t)}\)d'une fonction entre les instants \(t_1\) et \(t_2\) \(( t_2 > t_1)\) est de la forme :
\(\overline{f(t)}=\frac1{t_2-t_1}\int_{t_1}^{t_2}f(t)dt\)
Sur une alternance, la valeur moyenne du courant sera :
\(\color{blue}\overline{i(t)}\color{black}=\frac1{T/2}\int_0^{T/2}i(t)dt=\frac1{T/2}\int_0^{T/2}I_m\sin\omega tdt\)
\(=\color{blue}-\frac2T\frac{I_m}{\omega}[\cos\omega t]_0^{T/2}~~\color{red}\text{ (2 pts)}\)
\(\color{blue}\overline{i(t)}\color{black}=-\frac2T\frac{I_mT}{2\pi}[\cos\frac{\omega T}2-\cos 0]=\color{blue}\frac{2I_m}{\pi}~~\color{red}\text{ (2 pts)}\)