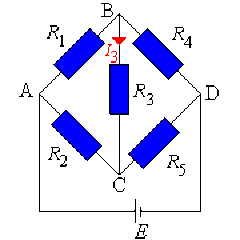
Loi des mailles
Partie
Question
En adoptant un sens de parcours, inverse du "sens trigonométrique classique", exprimer la loi des mailles dans : \(ABCA\), \(BDCB\) et \(ACDA\).
Aide simple
Loi des mailles : \(\color{blue} \underset{k}{\sum} R_{k} I_{k} = \underset{k}{\sum} E_{k}\)
La somme algébrique des chutes de tension dans une maille est égale à la somme algébrique des f.e.m. des sources existantes dans cette maille.
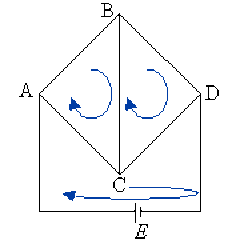
Aide détaillée
Pour la maille \(ABCA\), nous avons : \(R_{1}I_{1} + R_{3}I_{3} - R_{2}I_{2} = 0\)
Solution détaillée
Pour les trois mailles nous aurons :
\((ABCA) : R_{1}I_{1} + R_{3}I_{3} - R_{2}I_{2} = 0\)
\((BDCB) : R_{4}I_{4} - R_{5}I_{5} - R_{3}I_{3} = 0\)
\((ACDA) : R_{2}I_{2} + R_{5}I_{5} = E\)