Méthode de Cramer
Partie
Question
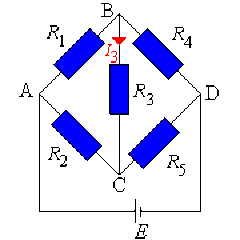
Calculer les courants \(I_{2}\), \(I_{3}\) et \(I_{4}\) par résolution du système selon la méthode de Cramer.
En déduire les courants \(I_{1}\), \(I_{5}\) et \(I\), ainsi que les tensions entre deux noeuds du circuit.
Aide simple
Pour le calcul de \(\Delta\), choisir de préférence la ligne ou la colonne comprenant un zéro.
Aide détaillée
Exprimer le courant \(I_{k} = \Delta_{k} / k\) traversant la résistance \(R_{k}\) en vous servant du déterminant \(\Delta_{k}\) de la matrice \([R]\) obtenu en remplaçant la kième colonne de \([R]\) par la matrice colonne \([U]\).
Solution simple
Le calcul du déterminant conduit après factorisation à :
\(\Delta = R_{1} R_{2} ( R_{3} + R_{4} + R_{5}) + R_{4} R_{5} ( R_{1} + R_{2} + R_{3} ) + R_{3} (R_{1} R_{5} + R_{2}R_{4}) = 2,4105.10^{9}~\Omega^{3}\)
Les courants étant :
\(I_{2} = \frac{E}{\Delta} \left[ R_{4} (R_{1} + R_{3}) + R_{1} (R_{3} + R_{5}) \right] \approx 6,852~\textrm{mA}\)
\(I_{3} = \frac{E}{\Delta} \left[ R_{2}R_{4} - R_{1}R_{5} \right] \approx 0,894~\textrm{mA}\)
\(I_{4} = \frac{E}{\Delta} \left[ R_{2} (R_{3} + R_{5}) + R_{5} (R_{1} + R_{3}) \right] \approx 6,469~\textrm{mA}\)
Solution détaillée
Calcul du déterminant \(\Delta\) de la matrice \([R]\) :
\(\Delta =\left| \begin{matrix} -R_{2} & (R_{1} + R_{3}) & R_{1} \\ -R_{5} & -(R_{3} + R_{5}) & R_{4} \\ (R_{2} + R_{5}) & R_{5} & 0 \end{matrix} \right|\)
La dernière colonne, comprenant un zéro, sera choisi pour développer les calculs :
\(\begin{array}{r l} \Delta & = R_{1} \left| \begin{matrix} -R_{5} & - (R_{3} + R_{5}) \\ R_{2} + R_{5} & R_{5} \end{matrix} \right| - R_{4} \left| \begin{matrix} -R_{2} & R_{1} + R_{3} \\ R_{2} + R_{5} & R_{5} \end{matrix} \right| \\ & = R_{1} \Big[ -R_{5}^{2} + (R_{2} + R_{5})(R_{3} + R_{5}) \Big] - R_{4} \Big[ -R_{2} R_{5} - (R_{1} + R_{3})(R_{2} + R_{5}) \Big] \end{array}\)
En développant, nous obtenons :
\(\begin{array}{r l} \color{red} \Delta & = -R_{1}R_{5}^{2} + R_{1}R_{2}R_{3} + R_{1}R_{3}R_{5} + R_{1}R_{2}R_{5} + R_{1}R_{5}^{2} + R_{2}R_{4}R_{5} + R_{1}R_{2}R_{4} + R_{2}R_{3}R_{4} + R_{1}R_{4}R_{5} + R_{3}R_{4}R_{5} \\ & \color{red} = R_{1}R_{2} (R_{3} + R_{4} + R_{5}) + R_{4}R_{5} (R_{1}+ R_{2} + R_{3}) + R_{3} (R_{1}R_{5} + R_{2}R_{4}) \end{array}\)
Application numérique : \(\Delta = 2,394 . 10^{9}~ \Omega^{3}\)
Calcul des courants \(I_{2}\), \(I_{3}\) et \(I_{4}\) :
Par définition, \(I_{k} = \Delta_{k} / \Delta\),
d'où :
\(I_{2} = \frac{\left| \begin{matrix} 0 & (R_{1} + R_{3}) & R_{1} \\ 0 & -(R_{3} + R_{5}) & R_{4} \\ E & R_{5} & 0 \end{matrix} \right|}{\Delta} = \frac{E}{\Delta} \left| \begin{matrix} (R_{1} + R_{3}) & R_{4} \\ -(R_{3} + R_{5}) & R_{4} \end{matrix} \right|\)
Ainsi, \(\color{blue}I_{2} \color{black}= \frac{E}{\Delta} \Big( R_{4}(R_{1} + R_{3}) + R_{1}(R_{3} + R_{5}) \Big) \approx \color{blue} 6,852~\textrm{mA}\)
Pour visualiser la valeur expérimentale de \(I_{2}\), c'est ici[6].
\(I_{3} = \frac{\left| \begin{matrix} -R_{2} & 0 & R_{1} \\ -R_{5} & 0 & R_{4} \\ R_{2} + R_{5}& E & 0 \end{matrix} \right|}{\Delta} = \frac{E}{\Delta} \left| \begin{matrix} -R_{2} & R_{1} \\ -R_{5} & R_{4} \end{matrix} \right|\)
Ainsi, \(\color{blue}I_{3} \color{black}= \frac{E}{\Delta} \Big( R_{2}R_{4} - R_{1}R_{5} \Big) \approx \color{blue} 0,894~\textrm{mA}\)
Pour visualiser la valeur expérimentale de \(I_{3}\), c'est ici[6].
\(I_{4} = \frac{\left| \begin{matrix} -R_{2} & (R_{1} + R_{3}) &0 \\ -R_{5} & -(R_{3} + R_{5}) & 0 \\ R_{2} + R_{5}& R_{5} & E \end{matrix} \right|}{\Delta} = \frac{E}{\Delta} \left| \begin{matrix} -R_{2} & R_{1} + R_{3}\\ -R_{5} & -( R_{3} + R_{5}) \end{matrix} \right|\)
Ainsi, \(\color{blue}I_{4} \color{black}= \frac{E}{\Delta} \Big( R_{2}( R_{3} + R_{5}) + R_{5}( R_{1} + R_{3})\Big) \approx \color{blue} 6,469~\textrm{mA}\)
Pour visualiser la valeur expérimentale de \(I_{4}\), c'est [8] [6] [7] ici[6].