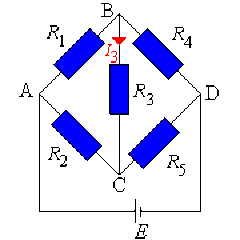
Loi d'ohm
Partie
Question
En choisissant \(I_{2}\), \(I_{3}\) et \(I_{4}\) comme variables mettre sous forme matricielle le système obtenu par la loi des mailles.
Aide simple
Ramener le système de 3 équations sous la forme \([R] [I] = [V]\), avec :
\([R]\) : matrice \(3 × 3\);
\([I]\) et \([V]\) : matrices colonnes.
Aide détaillée
Après substitution de \(I_{1}\) nous avons pour la maille \(ABCA\) : \(-R_{2}I_{2} + (R_{1} + R_{3}) I_{3} + R_{4}I_{4} = 0\)
Solution simple
Le système obtenu pour les trois mailles est :
\(\left\{ \begin{array}{l c l}-R_{2}I_{2} + (R_{1} + R_{3}) I_{3} + R_{1} I_{4} & = & 0 \\ -R_{5}I_{2} - (R_{3} + R_{5}) I_{3} + R_{4} I_{4} & = & 0 \\ (R_{2} + R_{5}) I_{2} + R_{5} I_{3} & = & E \\ \end{array}\right.\)
Solution détaillée
Substitution \(I_{1}\) et \(I_{5}\) dans les équations des mailles :
\(\left\{\begin{array}{r c l} R_{1}(I_{3} + I_{4}) + R_{3} I_{3} - R_{2} I_{2} & = & 0 \\ R_{4}I_{4} - R_{5} (I_{2} + I_{3}) - R_{3}I_{3} & = & 0 \\R_{2}I_{2} + R_{5}(I_{2} + I_{3}) & = & E \\\end{array} \right.\),
Ordonnons le système :
\(\left\{\begin{array}{r c l} -R_{2}I_{2} + (R_{1} + R_{3}) I_{3} + R_{1} I_{4} & = & 0 \\ R_{4}I_{4} - R_{5}I_{2} -(R_{3} + R_{5})I_{3} & = & 0 \\(R_{2} + R_{5})I_{2} + R_{5}+ I_{3} & = & E \\\end{array} \right.\);
d'où la forme matricielle :
\(\color{blue} \begin{pmatrix} -R_{2} & (R_{1} + R_{3}) & R_{1} \\ -R_{5} & -(R_{3} + R_{5}) & R_{4} \\ (R_{2} + R_{5}) & R_{5} & 0 \end{pmatrix} \begin{pmatrix} I_{2} \\ I_{3} \\ I_{4} \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ E \end{pmatrix}\)