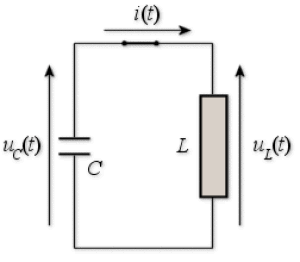
Oscillateur électrique : circuit oscillant (L,C)
Conditions initiales
Le condensateur est chargé de telle façon que \(q(t = 0) = q_0 > 0\) soit la charge de l'armature positive (rappelons que \(q_0 = C~u_C(t = 0)~\)) ; l'interrupteur étant ouvert, l'intensité initiale est nulle \(i (t = 0)= 0\). A l'instant initial le circuit est fermé.
Mise en équation du système, équation en charge
En choisissant les tensions et l'intensité instantanées comme indiqué sur le schéma et en exprimant la loi d'Ohm aux bornes des dipôles \(L\) et \(C\), (compte tenu des conventions de signes des circuits électriques), il vient :
\(u_L(t) = u_C(t) \Rightarrow L \frac{di(t)}{dt} = -\frac{1}{C} \int i(t) ~dt\)
Sachant que \(q(t) = Cu_C(t)\), on en déduit \(\frac{dq(t)}{dt} = C \frac{du_C (t)}{dt} = - i(t)\) et \(\frac{d^2q(t)}{dt^2} = - \frac{di(t)}{dt}\)
On en déduit facilement l'équation en \(q : L\frac{d^2q}{dt^2} + \frac{1}{C}q = 0\) ou
\(q" + \frac{1}{C}q = 0\)
Cette équation est du type oscillateur harmonique, de pulsation propre
\(\omega_0 = \sqrt{\frac{1}{LC}}\)
de solution générale \(q(t) = q_m \cos (\omega_0 t + \varphi)\) et compte tenu des conditions initiales la solution finale s'écrit
\(q(t) = q_0 \cos \omega_0t\).
La charge \(q(t)\) oscille entre les valeurs \(q_0\) et \(-q_0\), le condensateur se décharge et se charge alternativement, d'où le nom de circuit oscillant (remarquons qu'il n'y a pas de résistance dans le circuit, il n'y a pas d'amortissement).
Autres expressions
On déduit des résultats précédents les équations :
\(i(t) = -\frac{dq}{dt} = q_0 \omega_0 \sin \omega_0~t\)
\(i" + \frac{1}{LC}i = 0\) (équation en \(i\))
\(u_L(t) = u_C(t) = L\frac{di}{dt} = L ~q_0 ~\omega^2_0~ \cos \omega_0 t\)
\(u"_C + \frac{1}{LC}u_C = 0\) (équation en \(u_C\) )