Autres oscillateurs mécaniques
Les positions sont définies par rapport aux positions d'équilibre.
Système [masse, ressort] vertical
\(\vec e_x\) et \(l_e\) désignent respectivement les longueurs à vide et à l'équilibre, du ressort. Posons \(Y = l_e + y\) (avec \(Y = \overline{O_1M}(t)\), \(l_e = \overline{O_1O}\), \(y = \overline{OM}(t)\)), on montre que
\(y" + \frac{k}{m}y=0\) ,
la pulsation propre étant \(\omega_0 = \sqrt{\frac{k}{m}}\).
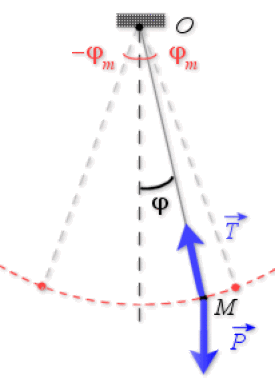
Pendule simple [fil de longueur constante, masse m]
Plusieurs méthodes conduisent à l'équation de l'oscillateur. L'une d'elles consiste à appliquer le théorème du moment cinétique calculé par rapport au point \(O\), les forces appliquées à la masse étant le poids \(\vec P\) et la tension \(\vec T\) du fil, il vient :
\(\frac{d}{dt}(\overrightarrow{OM} \wedge m\vec v) = \overrightarrow{OM} \wedge (\vec P + \vec T)\)
La masse \(m\) décrivant un arc de cercle de centre \(O\) et de rayon l et en exprimant la vitesse et l'accélération de \(m\) dans le repère polaire, on obtient l'équation satisfaite par la variable \(\varphi(t)\) :
\(ml^2\varphi" = - mgl \sin \varphi\) soit \(\varphi" + \frac{g}{l} \sin \varphi = 0\).
En considérant l'approximation des petits angles,
\(\sin \varphi \approx \varphi\), l'équation devient :
\(\varphi" + \frac{g}{l} \varphi = 0\) ,
équation d'un oscillateur harmonique de pulsation propre \(\omega_0 = \sqrt{\frac{g}{l}}\) (\(g\) étant l'accélération de la pesanteur).
Pendule de torsion [tige déformable, masses m]
Désignons par \(C\) la constante de torsion de la tige et par \(I\) le moment d'inertie. On montre que :
\(\varphi" + \frac{C}{I}\varphi = 0\)
\(~~\omega_0= \sqrt{\frac {C}{I}}\).