Etude de l'énergie

L'énergie totale ou énergie mécanique, notée \(E\), de l'oscillateur harmonique de type mécanique étudié, est égale à la somme des énergies cinétique et potentielle de la masse \(m\), notées respectivement \(E_c\) et \(E_p\) ; \(E_p\) est l'énergie potentielle associée à la force de rappel du ressort, soit :

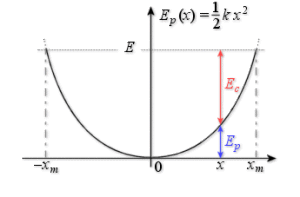
\(E = E_c + E_p\) \(\qquad\) où\(\qquad\) \(E_c(t) = \frac{1}{2}mv^2(t)\) \(\qquad\)et \(\qquad\) \(E_p(t) = \frac{1}{2}k x^2 (t)\)

(l'origine des énergies potentielles est choisie ici en \(x = 0\))

Comme \(~x(t) = x_m~\cos (\omega_0 t + \varphi)~\) et \(~v(t) = x'(t) = - \omega_0~x_m ~\sin( \omega_0~t +\varphi)~\), on en déduit

\(~E = \frac{1}{2}~m ~\omega_0^2~ x_m^2~\sin^2(\omega_0t + \varphi) + \frac{1}{2} k ~x_m^2 \cos^2 (\omega_0t + \varphi)~\) (avec \(\omega_0^2 = \frac{k}{m}\)).

Finalement, \(\qquad\) \(E = \frac{1}{2}~ m ~\omega_0^2 ~x_m^2 =\mathrm{ cste}\) \(\qquad\)ou\(\qquad\) \(~E = \frac{1}{2}~k~ x_m^2 = \mathrm{ cste}\)

(en rappelant que \(x_m^2 = x_0^2 + \frac{{x'}_0^2}{\omega_0^2} = \mathrm{ cste}\)).

Propriété

L'énergie mécanique du système est égale à une constante, notée \(E_0\), dont la valeur est déterminée par les conditions initiales :

\(E_0 = E_c(t = 0) + E_p(t = 0) = \frac{1}{2}~m~ {x'}_0^2 + \frac{1}{2} ~k ~x_0^2,\) valeur égale à \(~\frac{1}{2}~m~ \omega_0^2~x_m^2~\) ou à \(~\frac{1}{2}~k~ x_m^2.\)

Cette propriété est générale : quel que soit le type de système, l'énergie totale d'un système se comportant comme un oscillateur harmonique se conserve au cours des oscillations.

Graphes des fonctions Ec(t), Ep(t) et Ep(x) :

Les conditions initiales choisies sont \(x(t = 0) = x_0 > 0~\) et \(~x' (t = 0) = 0\).

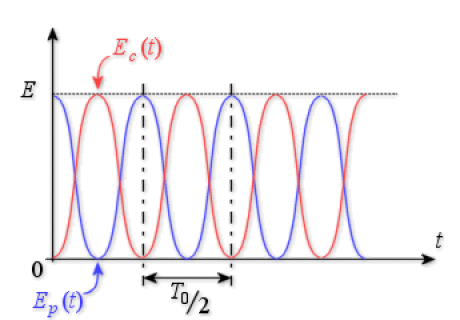
Variation temporelle de Ec(t) et de Ep(t) :

Les énergies cinétique et potentielle varient en fonction du temps, leur somme restant constante. Il y a, à tout instant, transformation d'énergie d'un type à l'autre.

\(E_c(t)\) et \(E_p(t)\) sont des fonctions sinusoïdales de période \(T_0 / 2\) et de valeur moyenne \(E/2\).

Variation spatiale de Ep(x) :

\(E_c\) et \(E_p\), définies par les expressions précédentes, ont des valeurs positives ou nulles ; l'énergie mécanique est fixée à la valeur \(E\) déterminée par les conditions initiales. Le graphe montre que \(-x_m \le x \le x_m~\), les oscillations de \(m\) sont limitées à ce domaine.