Energie
Durée : 4 mn
Note maximale : 4
Question
On considère une bille de masse\(m\)accrochée à l'extrémité d'un ressort vertical. La figure ci-dessous représente les variations respectives de l'énergie cinétique\((E_{c})\)et de l'énergie potentielle\((E_{p})\)au cours du temps de l'oscillateur.
Tracer la courbe de l'énergie mécanique de l'oscillateur et déterminer la période des oscillations. (2 pts)
Expliciter\(E_{c}\)et\(E_{p}\) . (2 pts)

Solution
1. (2 pts) L'énergie mécanique est égale à la somme de l'énergie cinétique et de l'énergie potentielle élastique :\(\qquad\) \(E_{m} = E_{c} + E_{p}\)
Sachant que l'énergie mécanique est constante, si on cherche à la tracer sur la figure qui est présentée, il suffit de localiser l'énergie cinétique maximale (à ce moment l'énergie potentielle est nulle) ou bien l'énergie potentielle maximale (à ce moment, l'énergie cinétique est nulle) et de tracer\(E_{m}\)puisque :
\(E_{m} = E_{c}^{\textrm{max}} +E_{p}^{\textrm{min}}\) ou\(E_{m} = E_{c}^{\textrm{min}} +E_{p}^{\textrm{max}}\)
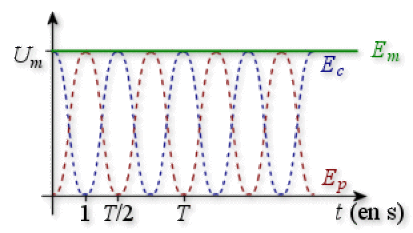
Pour déterminer la période des oscillations à partir du graphe des énergies, il ne faut pas oublier que l'énergie cinétique et l'énergie potentielle élastique varient comme le carré de la vitesse (pour l'énergie cinétique) ou bien le carré de la position (pour l'énergie potentielle élastique). Cela signifie que la période des énergies est 2 fois plus petite que la période des oscillations. Sur la figure, on peut mesurer la période des énergies (cinétique ou potentielle), soit 2 secondes, on en déduit que la période des oscillations\(T\)vaut 4 secondes.
2. (2 pts) L'énergie cinétique s'écrit :\(\qquad\) \(E_{c} = \frac{1}{2}mv^{2}\)
où\(m\)représente la masse de la bille et\(v\)sa vitesse.
L'énergie potentielle s'écrit :\(\qquad\) \(E_{p} = \frac{1}{2}kx^{2}\)
où\(k\)représente la raideur du ressort et\(x\)la position de la bille.