Oscillations d'une masse liquide
Durée : 12 mn
Note maximale : 8
Question
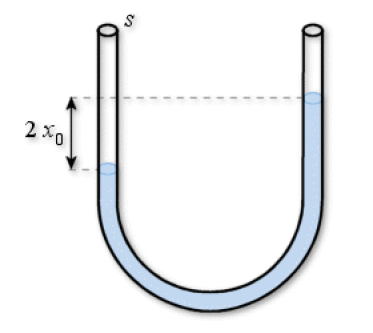
Un tube en U de section faible et uniforme\(s\)contient une masse\(m\)d'un liquide de masse volumique\(\rho\). La pression atmosphérique s'exerce sur les deux surfaces libres du liquide et on crée entre ces deux surfaces libres une dénivellation\(2x_{0}\)(voir figure).
On rappelle que l'énergie potentielle s'écrit :\(E_{p} = \textrm{masse}~\times~\textrm{accélération de la pesenteur}~\times~\textrm{hauteur}\).
Calculer la période des oscillations.
Solution
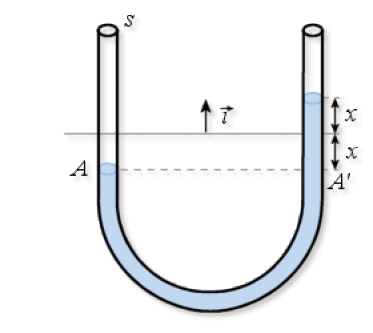
Lorsque le liquide est hors équilibre, la section du tube étant uniforme, toutes les particules de liquide ont une vitesse\(\vec{v}\). Le module de la vitesse, noté\(v\), s'écrit alors :\(\qquad\) \(v = \frac{dx}{dt}\)
L'énergie cinétique,\(E_{c}\), du fluide est :
\(E_{c} = \frac{1}{2}m\bigg(\frac{dx}{dt}\bigg)^{2}\)(1 pt)
On considère que l'on passe de l'équilibre\((x = 0)\)à la situation à l'instant\(t\)en élevant de\(x\)dans le champ de pesanteur une colonne de fluide de hauteur\(x\)et de section\(s\). L'énergie potentielle,\(E_{p}\) , s'écrit :
\(E_{p} = \textrm{masse}~\times~\textrm{accélération de la pesenteur}~\times~\textrm{hauteur} = \stackrel{\textrm{masse}}{\stackrel{ \uparrow }{(\rho sx)}}gx = \rho sgx^{2}\)(1 pt)
La conservation de l'énergie nous permet d'écrire alors :\(\qquad\) \(E_{c} + E_{p} =\textrm{cste}\)
\(\Leftrightarrow \frac{1}{2}m\bigg(\frac{dx}{dt}\bigg)^{2}+\rho sgx^{2} = \rho sgx_{0}^{2}\)(1 pt)
En dérivant par rapport au temps les deux membres de l'équation précédente nous obtenons :
\(2\times\frac{1}{2}m\frac{dx}{dt}\times\frac{d^{2}x}{dt^{2}} + 2\rho sgx\times\frac{dx}{dt} = 0\)
\(\Leftrightarrow\frac{d^{2}x}{dt^{2}} + \frac{2\rho sg}{m}x = 0\)(3 pts)
On reconnaît alors l'équation différentielle d'un oscillateur harmonique. La pulsation propre de cet oscillateur est déterminée à partir de :\(\qquad\) \(\omega_{0}^{2} = \frac{2\rho sg}{m}\)
La période propre est donc :
\(T_{0} = 2\pi\sqrt{\frac{m}{2\rho gs}}\)(2 pts)