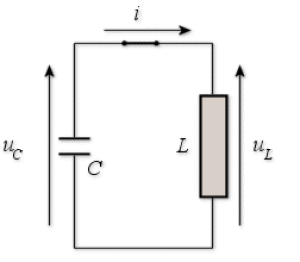
Circuit oscillant (L,C)
Partie
Question
Un condensateur de capacité \(C\) portant la charge \(q_{0}\) positive est relié à l'instant \(t=0\) aux bornes d'une bobine d'inductance \(L\) et de résistance interne négligeable.
Montrer que ce circuit est un circuit oscillant et déterminer la charge instantanée \(q(t)\) portée par le condensateur.
Quelle est la valeur de l'énergie électrique totale emmagasinée dans le circuit ?
Quelle est la valeur maximale de l'intensité au travers du circuit ?
On donne \(L = \textrm{0,5 mH}\) et \(C = 47 \textrm{ pF},\) \(q_{0} = \textrm{4,7 n C}.\)
Évaluer la fréquence d'oscillation du circuit, l'énergie totale, l'intensité maximale.
Rappel de cours
Relations entre les grandeurs instantanées :
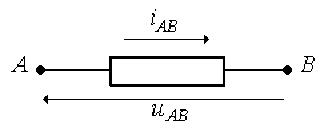
La différence de potentiel aux bornes d'une bobine d'inductance \(L\) et d'un condensateur de capacité \(C\) s'écrivent respectivement en fonction de l'intensité \(i_{AB}\) qui les traverse dans le sens de \(A\) vers \(B\) :
\(u_{L,AB} = L\frac{\textrm{d }i_{AB}}{\textrm{d }t}\) et \(u_{C,AB} = \frac{1}{C} \int i_{AB} \textrm{ d}t,\)
\(A\) et \(B\) étant les extrémités du dipôle.
La charge \(q\) du condensateur est liée à la \(ddp\) à ses bornes par : \(q=C ~u_{C,AB}\)
Les énergies instantanées emmagasinées dans la bobine et dans le condensateur s'écrivent respectivement :
\(E_{L} = \frac{1}{2} L i^{2}\) et \(E_{C} = \frac{1}{2} \frac{q^{2}}{C}\)
Solution détaillée
1. A tout instant la \(d.d.p.\) aux bornes de \(L\) est égale à celle aux bornes de \(C\) : \(u_{L} = u_{C}\) ou \(u_{L} - u_{C} = 0.\)
Compte tenu du choix du sens de l'intensité et des conventions habituelles de signe, il vient :
\(u_{L} = L \frac{\textrm{d}i}{\textrm{d}t} \), \(\qquad\) \(u_{C} = - \frac{1}{C} \int i \textrm{ d}t\)
\(\Rightarrow L \frac{\textrm{d}i}{\textrm{d} t} + \frac{1}{C} \int i \textrm{ d}t = 0 \) \(\qquad\) \((1)\)
Utilisons la variable \(q,\) sachant que \(q = C u_{C} = - \int i \textrm{ d}t,\) \(\frac{\textrm{d}q}{\textrm{d}t} = -i\) et \(\frac{\textrm{d}^{2}q}{\textrm{d}t^{2}} = - \frac{\textrm{d} i }{\textrm{d}t}.\)
L'équation (1) conduit à : \(\frac{\textrm{d}^{2}q}{\textrm{d}t^{2}} + \frac{1}{LC}q = 0.\)
Cette équation a la forme de celle de l'oscillateur harmonique \(q''+\omega_{0}^{2} q = 0,\) de pulsation propre \(\omega_{0} = \frac{1}{\sqrt{LC}},\) dont la solution générale s'écrit \(q(t) = q_{m} \cos(\omega_{0} t + \varphi).\)
Les constantes sont déterminées à partir des conditions initiales, \(q(t=0) = q_{0}\) et \(i(t=0) = q'(t=0)=0.\)
Ce qui permet d'écrire \(q_{0} = q_{m} \cos \varphi\) et \(0 = - \omega_{0} q_{m} \sin \varphi.\)
On en déduit \(\sin \varphi = 0\) et \(q_{m} = q_{0},\) d'où \(\varphi = 0,\) \(\cos \varphi\) devant être positif.
La charge obéit donc à la loi d'évolution \(q(t) = q_{0} \cos \frac{1}{\sqrt{LC}}t.\)
Remarquons que l'intensité est telle que \(i = - \frac{\textrm{d}q}{\textrm{d}t} = q_{0} \frac{1}{\sqrt{LC}} \sin \frac{1}{\sqrt{LC}}t.\)
2. Energie emmagasinée :
L'énergie électrique totale est égale à la somme des énergies emmagasinées sous formes magnétique dans la bobine et électrique dans le condensateur :
\(E = E_{L}(t) + E_{C}(t) = \frac{1}{2} L i^{2} + \frac{1}{2}\frac{q^{2}}{C}\)
Dans un circuit \((L,C)\) non amorti, l'énergie électrique totale se conserve. Elle est déterminée par la charge \(q_{0}\) du condensateur à l'instant \(t=0,\) l'intensité étant nulle à cet instant : \(E = \frac{1}{2}\frac{q_{0}^{2}}{C}.\)
L'intensité est maximale lorsque toute l'énergie est sous forme magnétique, donc si \(E\) représente l'énergie totale, alors \(i_{max} = \sqrt{\frac{2E}{L}}.\)
3. Application numérique :
De la relation \(\omega_{0} = 2 \pi f_{0} = \frac{1}{\sqrt{LC}}\) on déduit \(f_{0}^{2} = \frac {1}{4 \pi^{2}LC}.\)
Soit avec les données de l'exercice, \(f_{0}^{2} = 10^{12}\) et \(f_{0} = 10^{6} \textrm{ Hz} = 1 \textrm{ MHz}.\)
L'énergie électrique totale a pour valeur à l'instant \(t = 0\) :
\(E = \frac{1}{2}\frac{q_{0}^{2}(t=0)}{C} = \frac{1}{2}\frac{(\mathrm{4,7} . 10^{-9})^{2}}{47 . 10^{-12}} = \mathrm{0,235} . 10 ^{-6} \textrm{ J}\)
L'intensité maximale est \(i_{max} = \sqrt{\frac{2E}{L}} = \sqrt{\frac{q_{0}^{2}}{LC}} = \mathrm{30,6} . 10^{-3} \textrm{A}.\)