Oscillateur harmonique amorti, oscillations libres amorties

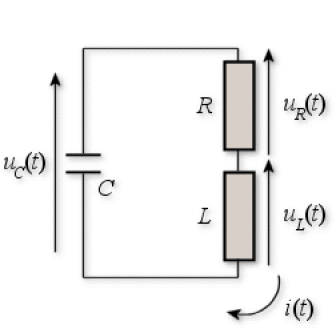
A l'instant initial le circuit est fermé ; désignons à un instant \(t\) par \(q(t)\) la charge du condensateur, par \(i(t)\) l'intensité du circuit et par \(u_L(t)\), \(u_R(t)\) et \(u_C(t)\) les tensions respectives aux bornes de la bobine, de la résistance et du condensateur.

\(u_L (t) + u_R(t) = u_C(t)\), explicitons les tensions \(L\frac{di}{dt} + Ri = -\frac{1}{C}\int i dt\), dérivons par rapport à \(t\), il vient,

\(L\frac{d^2i}{dt^2} + R \frac{di}{dt} + \frac{1}{C}i = 0\) ou

On pose : \(\frac{R}{L} = 2 \lambda\) et \(\frac{1}{LC} = \omega_0^2\)

L'équation différentielle ci-dessus est du type oscillateur harmonique amorti de coefficient d'amortissement \(\lambda = \frac{R}{2L}\) et de pulsation propre \(\omega_0 = \frac{1}{\sqrt{LC}}\).

Sachant que \(i(t) = - \frac{dq}{dt}\), d'après les conventions utilisées sur la figure, on établit facilement à partir de l'équation différentielle précédente l'équation satisfaite par la charge instantanée du condensateur :

Sachant que \(u_c(t) = \frac{q(t)}{C}\), on déduit de l'équation relative à la charge, l'équation satisfaite par la tension instantanée aux bornes du condensateur :