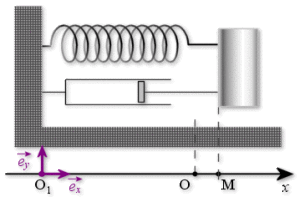
Système amorti [masse, ressort] horizontal
Partie
Un bloc de masse \(m\) est lié à l'extrémité libre d'un ressort de raideur \(k\), de longueur au repos \(l_{0}\), de masse négligeable et d'élasticité parfaite, l'autre extrémité \(O_{1}\) du ressort étant fixe.
Le seul mouvement possible pour le bloc est une translation suivant \(x\) ; on assimilera le bloc à un point matériel \(M\). Il glisse sur un plan horizontal sans frottement.
Le système est amorti. L'amortissement de type visqueux est représenté par un amortisseur qui exerce la force dissipative (ou force d'amortissement visqueux) \(\vec{F}_{d} = - \mu \vec{v}\) où \(\mu\) est un coefficient positif et \(\vec{v}\) le vecteur vitesse de \(M\).
Conventionnellement, l'amortisseur représente un amortissement visqueux. Un tel amortisseur est un dispositif qui s'oppose à toute déformation, proportionnellement à la vitesse de déformation. La force exercée s'écrit : \(\vec{F}_{d} = - \mu \vec{v}\).
Ne pas confondre le coefficient de proportionnalité \(\mu\) (appelé parfois coefficient visqueux) et la viscosité \(\eta\) d'un fluide.
On désigne par \(x(t)\) l'abscisse de \(M\) par rapport à sa position d'équilibre \(O\). A l'instant initial on écarte la masse de sa position d'équilibre jusqu'à la position \(x_{0}>0\) et on l'abandonne sans vitesse initiale. Les vecteurs unitaires respectivement associés aux axes horizontal et vertical sont notés \(\vec{e}_{x}\) et \(\vec{e}_{y}\).
Question
Montrer que l'équation différentielle du mouvement de \(M\) peut s'écrire :
\(\frac{\textrm{d}^{2}x}{\textrm{d}t^{2}} + 2 \lambda \frac{\textrm{d}x}{\textrm{d}t} + \omega_{0}^{2} x = 0\) (forme réduite)
Indiquer les expressions de \(\lambda\) et \(\omega_{0}^{2}\) en fonction des données du problème.
Solution détaillée
Le bilan des forces appliquées à la masse fait intervenir :
le poids \(\vec{P} = -mg \vec{e}_{y}\);
la réaction normale du plan \(\vec{R}_{n} = R_{n}\vec{e}_{y}\);
la force de rappel du ressort \(\vec{F}_{r} = -k (l - l_{0}) \vec{e}_{x}\) exprimée en fonction de \(x : \vec{F}_{r} = -k ~x ~\vec{e}_{x}\).
la force dissipative \(\vec{F}_{d} = - \mu \vec{v} = - \mu \frac{\textrm{d} x}{\textrm{d} t } \vec{e}_{x}\).
En supposant le repère galiléen, le principe fondamental de la mécanique permet d'écrire l'équation différentielle du mouvement :\(m \vec{\gamma} = \vec{P} + \vec{R}_{n} + \vec{F}_{r} + \vec{F}_{d}\).
Cette équation vectorielle se projette sur les directions \(\vec{e}_{x}\) et \(\vec{e}_{y}\) conduisant respectivement aux équations suivantes (en rappelant que \(\vec{e}_{x} . \vec{e}_{y} = 0\) et \(\vec{e}_{y} . \vec{e}_{y} = 1\)) :
suivant \(\vec{e}_{x}\) : \(m \frac{ \textrm{d}^{2} x}{\textrm{d} t^{2}} = - k~x - \mu \frac{\textrm{d}x}{\textrm{d} t}\),
suivant \(\vec{e}_{y}\) : \(0 = - mg + R_{n}\).
On pose \(\frac{\mu}{m} = 2 \lambda\) et \(\frac{k}{m} = \omega_{0}^{2}\) , l'équation de mouvement s'écrit :
\(\frac{\textrm{d}^{2}x}{\textrm{d} t^{2}} + 2 \lambda \frac{\textrm{d} x}{\textrm{d} t} + \omega_{0}^{2} x = 0\)
Question
Équation horaire du mouvement de \(M\) : dans le cas où le mouvement de \(M\) est oscillatoire, déterminer la solution \(x(t)\) de l'équation différentielle qui satisfait aux conditions initiales.
Aide méthodologique
Calculer le discriminant réduit. A quelle condition le mouvement de \(M\) est-il oscillatoire ? Comment désigne-t-on ce régime ?
Donner la forme de la solution générale de l'équation du mouvement.
Exprimer cette solution en fonction de l'amplitude \(x_{m}\), de \(\lambda\), de la phase \(\varphi\) et de la pseudo-pulsation \(\omega_{1}\) que l'on définira.
Ecrire l'expression de la pseudo-période \(T_{1}\) en fonction de \(\omega_{0}\) et de \(\lambda\).
En tenant compte des conditions initiales, déterminer les constantes \(x_{m}\) et \(\varphi\).
Solution détaillée
Le mouvement est oscillatoire si le discriminant réduit de l'équation caractéristique est négatif : \(\Delta ' = \lambda^{2} - \omega_{0}^{2} <0\). La condition s'écrit \(\omega_{0} > \lambda\). Ce régime oscillatoire amorti est dit pseudo-périodique.
La solution générale de l'équation, avec \(\Delta ' <0\), s'écrit sous la forme :
\(x(t) = x_{m} e^{-\lambda t} \cos(\omega_{1} t + \varphi)\), avec \(\omega_{1} = \sqrt{\omega_{0}^{2} - \lambda^{2}}\)
Les conditions initiales s'écrivent \(x(t = 0) = x_{0}\) et \(\dot{x} (t = 0) = 0\). On rapporte ces valeurs dans les expressions de la solution générale et de sa dérivée. La méthode est classique (calcul de \(x_{m} \cos \varphi\) et de \(x_{m} \sin \varphi\), puis élimination de \(\varphi\)) :
\(x(t = 0) = x_{0} = x_{m} \cos \varphi\)
\(\dot{x}(t = 0) = 0 = - \lambda x_{m} \cos \varphi - \omega_{1} x_{m} \sin \varphi\)
d'où \(x_{m}^{2} = x_{0}^{2} ( 1 + \frac{\lambda^{2}}{\omega_{0}^{2} - \lambda^{2}} )\) et \(\tan \varphi = - \frac{\lambda}{\sqrt{\omega_{0}^{2} - \lambda^{2}}}\) \((\varphi \textrm{ modulo } \pi)\)
La pseudo-période de ce mouvement est \(T_{1} = \frac{2 \pi}{\omega_{1}} = \frac{2 \pi}{\sqrt{\omega_{0}^{2} - \lambda^{2}}}\).
Question
Application numérique :
On donne \(m = 1 \textrm{ kg},\) \(l_{0} = 60 \textrm{ cm},\) \(k = 300 \textrm{ N m}^{-1},\) \(x_{0} = 20 \textrm{ cm},\) \(\mu = 30 \textrm{ N m}^{-1} \textrm{s}.\)
Calculer l’ensemble des caractéristiques de l'oscillateur : pseudo-période, temps de relaxation, décrément logarithmique, facteur de qualité, amplitude et phase.
Donner l'expression numérique de \(x(t)\). Tracer le graphe de \(x(t)\).
Aide méthodologique
Déterminer la dimension de \(\mu\), coefficient visqueux, et justifier l'unité employée.
Calculer le temps de relaxation \(\tau_{r}\) (relatif à l'énergie), le décrément logarithmique \(\delta = \lambda T_{1}\), et le facteur de qualité \(Q\) (on rappelle que \(\tau_{r} = \frac{m}{\mu} = \frac{1}{2 \lambda}\) et que \(Q = \omega_{0} \tau_{r}\)).
Calculer \(\omega_{1}\), \(T_{1}\), \(x_{m}\) et \(\varphi\).
Écrire l'expression numérique de \(x(t)\).
Solution détaillée
Le temps de relaxation et le facteur de qualité ont pour valeur, \(\tau_{r} = \textrm{0,033 s}\) et \(Q = \mathrm{0,57}\). Le décrément logarithmique a pour valeur \(\delta = \mathrm{10,87}\).
Les valeurs numériques sont les suivantes, en unités du système international (S.I.),\(\varphi\) étant exprimé en radians :
\(\omega_{0} = \textrm{17,3 rad.s}^{-1}\)
\(\lambda = 15 \textrm{ rad.s}^{-1}\) \(\omega_{1} = \textrm{8,66 rad.s}^{-1}\) \(T_{1} = \textrm{0,725 s}\)
\(x_{m} = \textrm{0,4 m}\)
\(\tan \varphi = -\sqrt{3}~~\)
\(~~\varphi = - \frac{\pi}{3} = -\mathrm{1,047}\)
(compte tenu de \(\cos \varphi = \frac{x_{0}}{x_{m}} >0\))
Dimension et unité du coefficient \(\mu\) : la relation \(\vec{F}_{d} = - \mu \vec{v}\) permet de dire que la dimension de \(\mu\) est celle du groupement \(\frac{F_{d}}{v}\), soit le rapport d'une force à une vitesse.
On écrit donc \([\mu] = \frac{MLT^{-2}}{LT^{-1}} = MT^{-1}\), il est donc normal d'utiliser pour unité soit des \(\textrm{kg.s}^{-1}\), soit des \(\textrm{N.m}^{-1}.\textrm{s}\).
L'équation horaire a pour expression : \(x(t) = \mathrm{0,4} e^{-15 ~t} \cos(\mathrm{8,66} ~t - \mathrm{1,047})\).
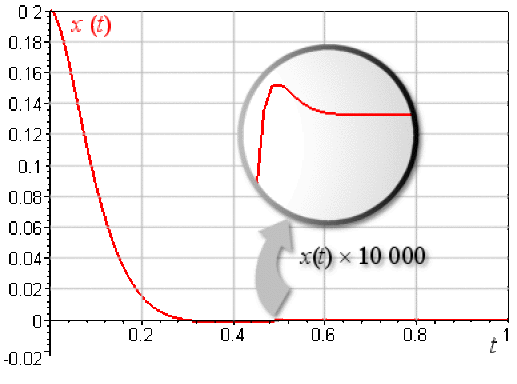
La figure montre que l'amplitude des oscillations décroit très rapidement (\(\lambda<\omega_{0}\), mais \(\lambda\) proche de \(\omega_{0}\)). Une dilatation de l'échelle des ordonnées mettrait en évidence des petites oscillations entre \(t =\textrm{0,3 s}\) et \(t =\textrm{0,5 s}\). A partir de \(t = \textrm{0,5 s}\), le système revient à sa position d'équilibre \(( x(t) = 0)\).