Circuit série (R,L,C), décharge du condensateur
Partie
Un condensateur de capacité \(C\) portant la charge positive \(q_{0}\) est relié à l'instant \(t = 0\) aux bornes d'une bobine d'inductance \(L\) et de résistance interne \(R.\)
Question
Montrer que l'intensité \(i(t)\) du circuit et la charge \(q(t)\) du condensateur satisfont respectivement aux équations différentielles :
\(i'' + \frac{R}{L}i' + \frac{1}{LC}i = 0 \) \(\qquad , \qquad\) \(q'' + \frac{R}{L} q' + \frac{1}{LC} q = 0\)
Rappel de cours
Relations entre les grandeurs instantanées :
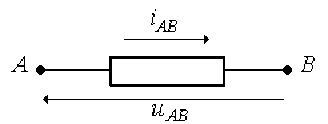
La différence de potentiel aux bornes d'une bobine d'inductance \(L\) et d'un condensateur de capacité \(C\) s'écrivent respectivement en fonction de l'intensité \(i_{AB}\) qui les traverse dans le sens de \(A\) vers \(B\) :
\(u_{L,AB} = L\frac{\textrm{d }i_{AB}}{\textrm{d }t}\) et \(u_{C,AB} = \frac{1}{C} \int i_{AB} \textrm{ d}t,\)
\(A\) et \(B\) étant les extrémités du dipôle.
La charge \(q\) du condensateur est liée à la \(ddp\) à ses bornes par : \(q=C ~u_{C,AB}\).
Solution détaillée
A tout instant la différence de potentiel aux bornes de \(C\) est égale à la somme des différences de potentiel aux bornes de \(R\) et de \(L\) :
\(u_{C} = u_{R} + u_{L}\) ou \(u_{R} + u_{L} - u_{C} = 0\)
Compte tenu du choix du sens de l'intensité et des règles de signes habituelles :
\(u_{R} = R ~i\), \(u_{L} = L \frac{\textrm{d} i}{\textrm{d} t}\) \(\qquad\) et \(\qquad\) \(u_{C} = - \frac{1}{C} \int ~i ~\textrm{d} t \Rightarrow R i + L \frac{d i} {d t} + \frac{1}{C} \int ~i ~\textrm{d} t = 0\) (1)
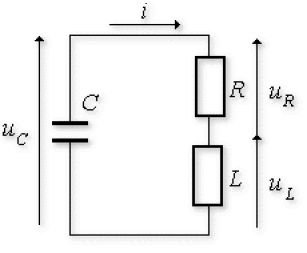
Représentation du circuit à un instant t
En dérivant l'équation (1) par rapport au temps et en ordonnant, on en déduit l'équation en « intensité » : \(\frac{\textrm{d}^{2} i }{\textrm{d}t^{2}} + \frac{R}{L} \frac{\textrm{d}i}{\textrm{d} t} + \frac{1}{LC} i = 0\) (2)
Introduisons la charge instantanée \(q(t)\) du condensateur.
Sachant que \(q = C ~u_{C}\), compte tenu de l'expression précédente de \(u_{C}\), on en déduit :
\(q = - \int i \textrm{ d} t\), \(\frac{\textrm{d}q}{\textrm{d}t} = -i\), \(\frac{\textrm{d}^{2}q}{\textrm{d}t^{2}} = - \frac{\textrm{d} i }{\textrm{d}t}\)
L'équation (1) conduit à l'équation relative à la « charge » : \(\frac{\textrm{d}^{2}q}{\textrm{d} t^{2}} + \frac{R}{L} \frac{\textrm{d}q}{\textrm{d} t} + \frac{1}{LC}q = 0\) (3)
Question
En déduire que le circuit étudié est un oscillateur harmonique amorti.
Déterminer le coefficient d'amortissement \(\lambda\) et la pulsation propre \(\omega_{0}\) du circuit.
Solution détaillée
On constate que les équations (2) et (3) décrivent un oscillateur harmonique amorti caractérisé par le coefficient d'amortissement \(\lambda = \frac{R}{2 L}\) et la pulsation propre \(\omega_{0} = \frac{1}{\sqrt{LC}}\).
Question
A quelles conditions le régime d'évolution est-il respectivement apériodique, critique et pseudo-périodique ?
Solution détaillée
Le discriminant réduit relatif à l'équation (2) ou à l'équation (3) s'écrit :
\(\Delta ' = \sqrt{\lambda^{2} - \omega_{0}^{2}} = \sqrt{\frac{R^{2}}{4 L^{2}} - \frac{1}{LC}}\)
Le régime est :
apériodique si \(\Delta ' >0\) , soit si \(\frac{R}{2L} > \frac{1}{\sqrt{LC}}\) ou \(R > 2 \sqrt{\frac{L}{C}}\)
critique si \(\Delta ' = 0\), soit si \(R = 2 \sqrt{\frac{L}{C}}\)
pseudo-périodique si \(\Delta ' < 0\), soit si \(R< 2 \sqrt{\frac{L}{C}}\)
Question
Dans le cas du régime pseudo-périodique, déterminer l'expression de \(q(t)\) (utiliser les deux conditions initiales relatives à la charge et à l'intensité : \(q(t=0)\) et \(i(t = 0)\)). En déduire \(i(t)\).
Solution détaillée
Dans le cas du régime pseudo-périodique, la solution générale de l'équation (3) s'écrit : \(q(t) = q_{m} e^{-\lambda t} \cos (\omega_{1} t + \varphi)\), la pseudo-pulsation s'écrivant \(\omega_{1} = \sqrt{\omega_{0}^{2} - \lambda^{2}}\).
Les conditions initiales \(q(t = 0) = q_{0}\) et \(i(t = 0) = - \bigg(\frac{\textrm{d}q}{\textrm{d}t} \bigg) _{t = 0}=0\) ou \(q'(t = 0) = 0\) permettent de calculer les deux constantes \(q_{m}\) et \(\varphi\).
La méthode est classique (calcul de \(q_{m} \cos \varphi\) et de \(q_{m} \sin \varphi\), puis élimination de \(\varphi\)). On obtient les résultats : \(q_{m} = \sqrt{q_{0}^{2} + \frac{\lambda^{2}}{\omega_{1}^{2}}}\) et \(\tan \varphi = \frac{- \lambda}{\omega_{1}}\) ( \(\varphi\) modulo \(\pi\) et \(\cos \varphi = \frac{q_{0}}{q_{m}} >0\) ) en rappelant que \(\lambda = \frac{R}{2L}\) et \(\omega_{1} = \sqrt{\frac{1}{LC} - \frac{R^{2}}{4 L^{2}}}\).
L'intensité se déduit de la relation \(i(t) = - \frac{\textrm{d} q(t)}{\textrm{d}t}.\) Remarquons que \(i(t)\) peut être calculé directement à partir de l'équation (2) compte tenu des conditions initiales.
Question
Exprimer en fonction de \(R, L\) et \(C\) le facteur de qualité \(Q\) du circuit.
Solution détaillée
La définition du facteur de qualité étant \(Q = \frac{\omega_{0}}{2 \lambda}\) (ou \(\omega_{0} \tau_{r}\)), il vient \(Q = \frac{1}{R} \sqrt{\frac{L}{C}}\).