Détermination expérimentale des grandeurs caractéristiques d'un oscillateur amorti
Partie
Question
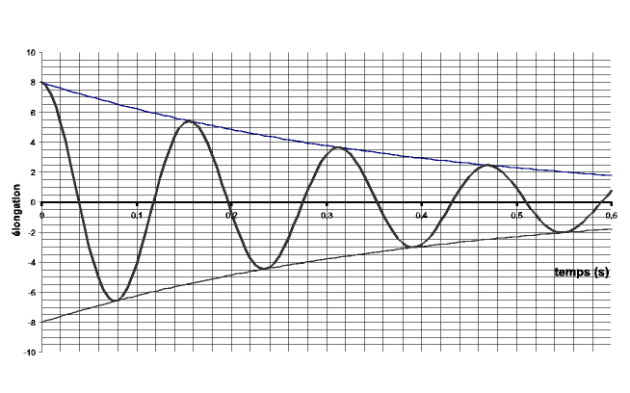
On réalise le relevé expérimental de la réponse d'un oscillateur en fonction du temps. On représente en plus sur le relevé, les courbes enveloppes des extrema.
D'après l'allure de la courbe précisez de quel type de régime il s'agit.
Mesurer le décrément logarithmique pour chaque pseudo-période ; s'agit-il d'un amortissement exponentiel ?
Déterminer les caractéristiques suivantes : pseudo-période, pseudo-pulsation, temps de relaxation, facteur de qualité. On rappellera les expressions littérales utilisées.
Rappel de cours
Quelques expressions utiles
On rappelle les expressions suivantes :
Décrément logarithmique : \(\delta = \ln \frac{x(t_{n})}{x(t_{n} + T_{1})} = \lambda T_{1}\)
Temps de relaxation (relatif à l'énergie) : \(\tau_{r} = \frac{1}{2 \lambda}\)
Facteur de qualité : \(Q = \omega_{0} \tau_{r}\)
Expression de \(Q\) en fonction de \(\delta\) : \(Q = \frac{\pi}{\delta}\sqrt{1 + \frac{\delta^{2}}{4\pi^{2}}}\)
Expression approchée : \(Q \approx \frac{\pi}{\delta}\)
Solution détaillée
Le régime est pseudo-périodique (sinusoïdal amorti).
On relève à partir du graphe les valeurs suivantes des extréma successifs :
\(\textrm{Temps}\)
\(\mathrm{0}\)
\(\mathrm{0,078}\)
\(\mathrm{0,155}\)
\(\mathrm{0,235}\)
\(\mathrm{0,312}\)
\(\mathrm{0,39}\)
\(\mathrm{0,47}\)
\(\textrm{Elongation}\)
\(\mathrm{8}\)
\(\mathrm{-6,6}\)
\(\mathrm{5,5}\)
\(\mathrm{-4,5}\)
\(\mathrm{3,8}\)
\(\mathrm{-3}\)
\(\mathrm{2,5}\)
Les rapports des élongations successives de même signe sont reportés dans le tableau suivant :
\(x(t_{n})\)
\(x(t_{n} + T_{1})\)
\(\delta = \ln \frac{x(t_{n})}{x(t_{n} + T_{1})}\)
\(\textrm{Elongations} >0\)
\(\mathrm{8}\)
\(\mathrm{5,5}\)
\(\mathrm{0,37}\)
\(\textrm{Elongations} >0\)
\(\mathrm{5,5}\)
\(\mathrm{3,8}\)
\(\mathrm{0,37}\)
\(\textrm{Elongations} >0\)
\(\mathrm{3,8}\)
\(\mathrm{2,5}\)
\(\mathrm{0,42}\)
\(\textrm{Elongations} <0\)
\(\mathrm{-6,6}\)
\(\mathrm{-4,5}\)
\(\mathrm{0,38}\)
\(\textrm{Elongations} <0\)
\(\mathrm{-4,5}\)
\(\mathrm{-3}\)
\(\mathrm{0,40}\)
Les décréments sont constants compte-tenu de la précision des mesures : l'amortissement est bien exponentiel. On propose pour valeur \(\delta = \mathrm{0,4}\pm \mathrm{0,03}\).
La pseudo-période est déterminée à partir des valeurs \(t = 0\) et \(t = \mathrm{0,47}\) correspondant à trois périodes : \(T_{1} = (\mathrm{0,16} \pm \mathrm{0,01})\textrm{ s}\). On en déduit la pseudo-pulsation \(\omega_{1} = \frac{2 \pi}{T_{1}} = (42 \pm 3) \textrm{ rad.s}^{-1}\).
Le décrément logarithmique est lié à l'amortissement \(\lambda\) par la relation \(\delta = \lambda T_{1}\). On en déduit \(\lambda = \textrm{2,66 rad.s}^{-1}\).
Le temps de relaxation \(\tau_{r} = \frac{1}{2\lambda}\) est ici \(\tau_{r} = \textrm{0,19 s}\).
Enfin le facteur de qualité peut s'exprimer en fonction du décrément, par la relation approchée \(Q \approx \frac{\pi}{\delta}\). L'application dans l'exercice conduit à \(Q \approx 8\).
Il est possible de déterminer \(Q\) à partir de sa définition \(Q = \omega_{0} \tau_{r}\), la pulsation propre \(\omega_{0}\) s'exprimant en fonction de \(\omega_{1}\) et \(\lambda\) par la relation \(\omega_{0} = \sqrt{\omega_{1}^{2} + \lambda^{2}}\). Connaissant les valeurs de \(\omega_{1}\), \(\lambda\) et \(\tau_{r}\), on en déduit \(\omega_{0} = \textrm{42 rad.s}^{-1}\) et \(Q = \textrm{7,98}\). Cette valeur est en accord avec la valeur approchée précédente \(Q \approx 8.\)
Remarque :
Le graphique utilisé a été généré en fait dans un tableur, et non relevé expérimentalement, en utilisant l'équation \(x(t) = 8 e^{-2,5 t} \cos (40 t).\)
Les valeurs exactes à déterminer sont donc :
\(\lambda = \textrm{2,5 s}^{-1},\) \(\omega_{1} = \textrm{39,9 rad.s}^{-1},\) \(T_{1} = \textrm{0,158 s},\) \(\delta = \textrm{0,393},\) \(\tau_{r} = \textrm{0,2 s}\) et \(Q = 8\)
La lecture des données à l'écran fournit une précision tout à fait convenable.