Application : forme initiale et vibrations de la corde
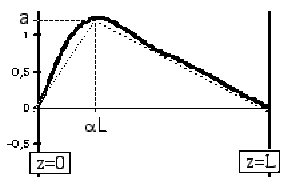
Soit une corde vibrante, dont les extrémités sont fixes et dont l'état initial est représenté ci-contre par une forme "presque triangulaire" : \(\psi(z,0)\).
On suppose de plus que les vitesses initiales sont toutes nulles.
La méthode annoncée au paragraphe précédent consiste à construire un prolongement périodique de \(\psi(z,0)\) tel que ce prolongement \(F(z)\) coïncide avec \(\psi(z,0)\) pour \(z \in [0,L]\) , mais soit défini \(\forall z\) réel.
La première question qui se pose est de savoir selon quels critères effectuer ce prolongement périodique. Les deux schémas ci-dessous montrent en effet qu'il existe au moins ces deux façons de réaliser un prolongement périodique de la fonction "presque triangle" définie sur \([0,L]\) par la forme de la corde \(\psi(z,0)\).
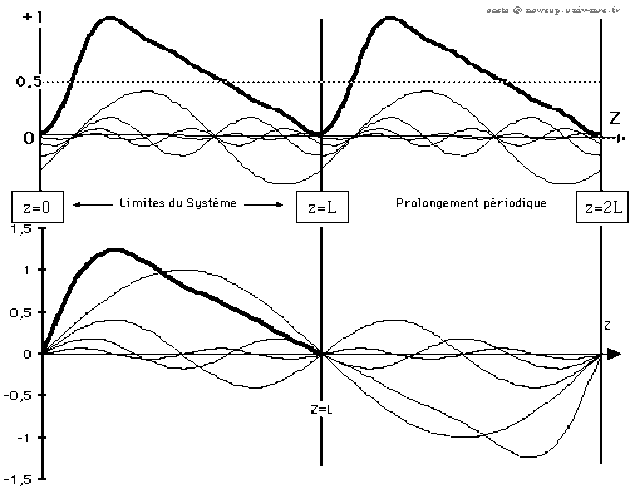
Ces schémas montrent en réalité la forme de la corde à l'état initial, obtenue par la somme des 4 premiers harmoniques non nuls de la décomposition en série de Fourier de fonctions triangles (selon 2 prolongements périodiques différents). Il n'est cependant pas évident, à priori, que chacun de ces développements convienne pour représenter la vibration du système à partir de ces différents prolongements.
Cette question sera traitée en exercice. Pour vous en convaincre, regardez tout de suite les vibrations obtenues à partir de chacun de ces deux prolongements.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
La deuxième question qui se pose est de savoir si le développement en série de Fourier du prolongement périodique choisi \(F(z)\), est constitué des mêmes coefficients que ceux intervenant dans \(\psi(z,0)\).
Puisque \(\psi(z,0)\) coïncide avec \(F(z)\) pour \(z \in [0,L]\), \(\psi(z,0)\) s'obtient simplement à partir de \(F(z)\) par une restriction à \([0,L]\) de l'intervalle de définition de \(F\).
Enfin, compte tenu du théorème (2) (§ C.I.b), l'unicité du développement (pour un prolongement périodique choisi et sur les fonctions de base utilisées) est assurée.
Le calcul des coefficients de Fourier sur la base des \(\sin (K_p.z)\) donne le résultat suivant :
\(b_p = \frac{2.a}{p^2 . \pi^2} ~ . ~ \frac{1}{\alpha . (1 - \alpha)} ~ . ~ \sin (p . \pi . \alpha)\)
ce qui permet de déterminer le rapport de l'amplitude \(b_p\) à celle du fondamental \(b_1\) :
\(\frac{b_p}{b_1} = \frac{1}{p^2} ~ . ~ \frac{\sin (p . \pi . \alpha)}{\sin (\pi . \alpha)}\)
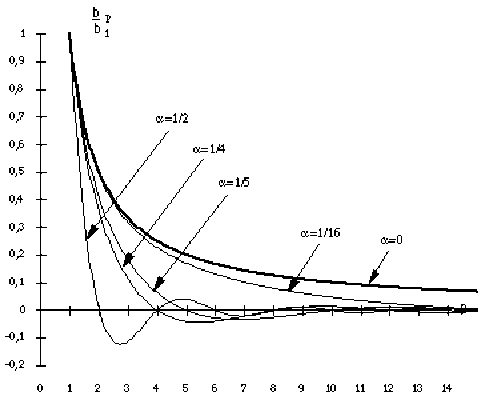
Les courbes enveloppes de ces rapports sont représentées sur le schéma suivant, pour plusieurs valeurs de \(a\) : \(0\), \(\frac{1}{16}\), \(\frac{1}{5}\), \(\frac{1}{4}\) ...
Remarque :
Pour certaines valeurs du coefficient \(\alpha\) certains harmoniques ont une amplitude nulle.
Pour \(\alpha = \frac{1}{4}\) par exemple, tous les harmoniques de rang multiple de \(4\) sont nuls.
Le cas \(\alpha = \frac{1}{2}\) donne :
pour \(p\) pair : \(\frac{b_p}{b_1} = 0\)
pour \(p\) impair (\(p=2n+1\)) : \(\frac{b_p}{b_1} = \frac{(-1)^n}{p^2}\)
Le cas \(\alpha = 0\) donne : \(\frac{b_p}{b_1} = \frac{1}{p}\)
La page "Enveloppe du module des rapports d'amplitude" représente l'enveloppe de ces coefficients.