Représentations en fréquence

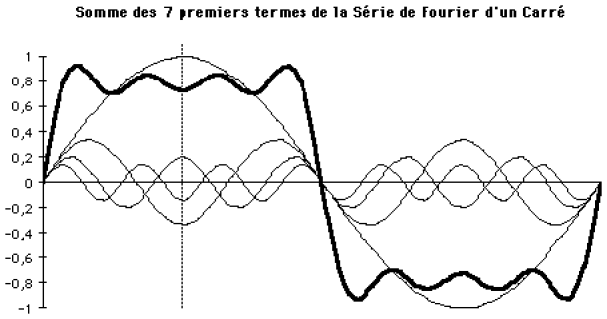
Le schéma suivant représente le graphe d'une fonction $F$ carré symétrique approximée par la somme des $4$ premiers termes non-nuls de sa série de Fourier.

L'origine choisie pour tracer ce graphe $\{z, F(z)\}$ fait de $F$ une fonction impaire.

Dans ce cas, sa série n'a de composante non-nulle que sur les fonctions de base en $\sin(K_p.z)$.

Avec un autre choix d'origine pour représenter cette forme carré, la fonction correspondante pourrait être paire : une translation d'origine de $\Delta z = \frac{\lambda}{4}$ correspond à un déphasage de :

$\displaystyle{K_p . \Delta z = \frac{K_p . \lambda}{4} = \frac{p . K_1. \lambda}{4} = \frac{p . 2 \pi}{\lambda} \frac{\lambda}{4} = \frac{p . \pi}{2}}$ ,

qui transforme tous les harmoniques $p$ impairs de type $\sin(K_p.z)$ en type $\cos(K_p.z)$ et donc la fonction impaire en fonction paire.

La translation inverse transformerait la fonction paire en fonction impaire.

Par exemple, si l'origine est à l'intersection de l'axe $z$ et de la droite verticale en pointillés, la forme carré sera alors le graphe d'une fonction $G$ paire.

Elle sera représentée sur les fonctions de base en $\cos(K_p.z)$.

On calculera en exercice les coefficients $A_p$ de la fonction impaire $F$ et les coefficients $B_p$ de la fonction paire $G$.

On vérifiera que les séries de $F$ et de $G$ ne comportent que les termes impairs.

On montrera la relation existant entre la valeur algébrique des composantes de $G$ sur les cosinus et de $F$ sur les sinus.

Avec un autre choix d'origine pour représenter cette forme carré, la fonction correspondante peut également être ni paire ni impaire : exprimer par exemple la série de Fourier de la fonction qui serait obtenue par une translation de $\lambda/6$.