Construction des hybrides sp
Partie
Question
On considère la molécule \(\mathrm{BeH_2}\). C'est une molécule linéaire symétrique que l'on place suivant l'axe \(\mathrm{Ox}\). L'atome de bérylium est à l'origine du repère. Le plan \(\mathrm{yOz}\) est un plan de symétrie.
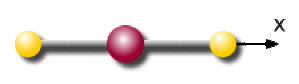
Les deux électrons de valence du bérylium sont décrits par deux orbitales hybrides \(\varphi_1\) et \(\varphi_2\) de type sp, composées des orbitales \(2\mathrm{s}\) et \(2\mathrm{p_x}\) de l'atome. Ces deux hybrides sont l'image l'une de l'autre par le plan de symétrie.
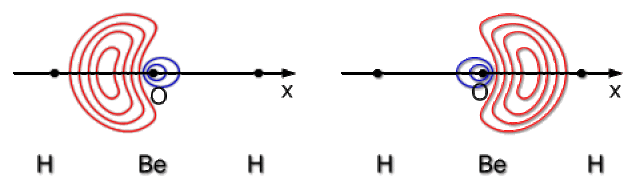
L'angle d'hybridation 2s-2p dans ces hybrides dépend de l'écart d'énergie entre les orbitales 2s et 2p et de la force relative des interactions avec l'hydrogène. On note cet angle \(\alpha\) que l'on suppose connu (la valeur de \(\alpha\) dépend des approximations que l'on peut faire sur le calcul des énergies). \(\alpha\) est relatif au mélange de l'orbitale 2s et d'une orbitale 2p orientée suivant une liaison BeH :
\(\varphi=\cos\alpha~2\mathrm{s}+\sin\alpha~2\mathrm{p}\)
1. Déterminer complètement la forme mathématique de ces 2 hybrides.
2. Calculer le recouvrement entre ces deux hybrides.
Aide simple
1. Les deux orbitales hybrides \(\varphi_1\) et \(\varphi_2\) se reflètent par rapport au plan \(\mathrm{yOz}\). On peut alors écrire :
\(\varphi_1(-\mathrm{x,y,z)=\varphi_2(x,y,z)}\)
2. Les orbitales atomiques pures sont normées.
Aide méthodologique
1. Il faut tenir compte de la symétrie de la molécule et des propriétés de symétrie des orbitales atomiques.
2. On utilise l'expression de l'intégrale de recouvrement entre deux orbitales et on décompose cette intégrale pour faire apparaître des intégrales de valeur connue.
Aide à la lecture
Les orbitales hybrides s'écrivent comme combinaisons linéaires des orbitales atomiques \(2\mathrm{s}\) et \(2\mathrm{p_x}\) du bore. Il s'agit de déterminer complètement les coefficients LCAO.
Solution détaillée
1. La première hybride ne contient que l'orbitale \(2\mathrm{s}\) et l'orbitale \(2\mathrm{p_x}\).
Elle s'exprime alors suivant l'expression :
\(\varphi_1=\cos\alpha~2\mathrm{s+\sin\alpha~2p_x}\)
Pour déterminer la seconde hybride, on utilise le fait que les deux hybrides sont l'image l'une de l'autre par le plan \(\mathrm{yOz}\) :
\(\varphi_2(\mathrm{x,y,z)=\varphi_1(-x,y,z)}\)
L'hybride \(\varphi_2\) s'écrit :
\(\varphi_2(\mathrm{x,y,z)=\cos\alpha~2s(-x,y,z)+\sin\alpha~2p_x(-x,y,z)}\)
L'orbitale\( \mathrm{2s}\) est de symétrie sphérique : \(2\mathrm{s(-x,y,z)=2s(x,y,z)}\)
L'orbitale \(\mathrm{2p_x}\) est antisymétrique : \(2\mathrm{p_x(-x,y,z)=-2p_x(x,y,z)}\)
Il vient alors :
\(\varphi_2(\mathrm{x,y,z)=\cos\alpha~2s(x,y,z)-\sin\alpha~2p_x(x,y,z)}\)
soit
\(\varphi_2\mathrm{=\cos\alpha~2s-\sin\alpha~2p_x}\)
2. L'intégrale de recouvrement entre les deux hybrides est :
\(\mathrm{S=\int_{espace}\varphi_1.\varphi_2~dv}\)
On développe cette intégrale en décomposant les hybrides :
\(\mathrm{S=\int_{espace}\left(\cos\alpha~2s+\sin\alpha~2p_x\right).\left(\cos\alpha~2s-\sin\alpha2p_x\right)dv}\)
\(\mathrm{S=\int_{espace}\left(\cos^2\alpha\times2s^2+\sin^2\alpha\times2p_x^2\right)dv}\)
\(\mathrm{S=\cos^2\alpha\int_{espace}2s^2~dv-\sin^2\alpha\int_{espace}2p_x^2~dv}\)
Les deux intégrales représentent les normes des orbitales \(\mathrm{2s}\) et \(\mathrm{2p_x}\). Elles valent 1 par définition. Il vient en définitive :
\(\mathrm{S=\cos^2\alpha-\sin^2\alpha}\)
Le recouvrement entre les deux hybrides dépend du mélange 2s-2p.