Caractérisation géométrique
Théorème :
Soit \(f\) une application d'un intervalle \(\mathcal I\) dans \(\mathbf R\) ; l'application \(f\) est convexe si et seulement si l'ensemble \(\mathcal E_f\) est convexe
On représente une fonction \(f\) convexe sur l'intervalle \([a,b]\) et son épigraphe.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Preuve :
On utilise le fait qu'un point d'un segment est barycentre à coefficients positifs des extrémités du segment.
Condition nécessaire
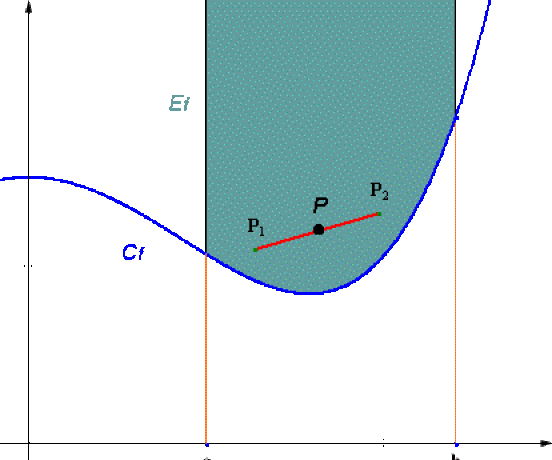
On suppose \(f\) convexe. Soient \(P_1(x_1,y_1)\) et \(P_2(x_2,y_2)\) deux points de \(E_f\) on a \(f(x_1)\le y_1\) et \(f(x_2)\le y_2\). Si \(P(x,y)\) est un point du segment \([P_1,P_2]\), alors il existe un réel \(\lambda\in[0,1]\) tel que : \(x=\lambda x_1+(1-\lambda)x_2,y=\lambda y_1+(1-\lambda)y_2\).
On a donc : \(y\ge\lambda f(x_1)+(1-\lambda)f(x_2)\).
L’hypothèse de convexité entraîne alors : \(\lambda f(x_1)+(1-\lambda)f(x_2)\ge f(\lambda x_1+(1-\lambda)x_2)=f(x)\),
d’où \(y\ge f(x)\) et le point \(P\) appartient à \(E_f\).
Condition suffisante
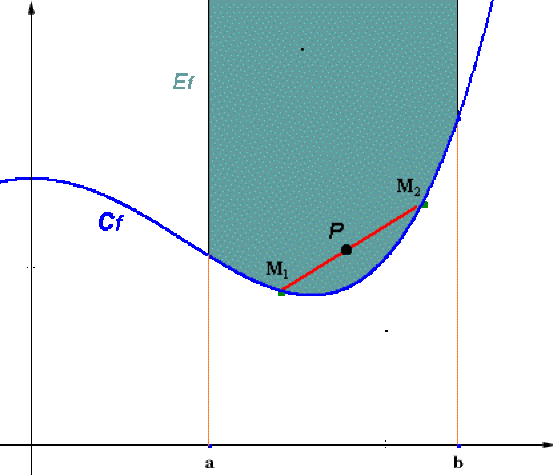
On suppose que \(E_f\) est convexe, ainsi, si \(M_1(x_1,f(x_1))\) et \(M_2(x_2,f(x_2))\) sont des points de \(C_f\) , ils appartiennent à \(E_f\) et le segment \([M_1,M_2]\) est inclus dans \(E_f\).
Soit \lambda\in[0,1], alors le point \(P(\lambda x_1+(1-\lambda)x_2,\lambda f(x_1)+(1-\lambda)f(x_2))\) appartient au segment \([M_1,M_2]\) et donc à \(E_f\), d’où :
\(f(\lambda x_1+(1-\lambda)x_2)\le\lambda f(x_1)+(1-\lambda)f(x_2)\).
Application : Inégalité de Jensen
Soient \(f\) une fonction convexe sur \(\mathcal I, x_1, x_2\cdots x_n\quad n\) points de \(\mathcal I\) et \(\lambda,\lambda_2,\cdots,\lambda_n,\quad n\) réels strictement positifs tels que\( \displaystyle{\sum_{i=1}^{n}\lambda_i=1}\). On a alors :
\(\displaystyle{f\left(\sum_{i=1}^{n}\lambda_ix_i\right)\leq\sum_{i=1}^{n}\lambda_if(x_i)}\)
Preuve :
On fait un raisonnement par récurrence sur \(n\).
La propriété est vraie pour \(n = 1\) et \(n = 2\). Supposons la propriété vraie pour un rang \(n\ge2\).
Soient \(x_1, x_2 …x_{n+1} n + 1\) points de \(I\) et \(\lambda_1,\lambda_2,...,\lambda_{n+1} n + 1\) réels strictement positifs tels que \(\displaystyle{\sum_{i=1}^{n+1}}\lambda_i=1\).
On définit \(y\) par l’égalité : \(\left(\displaystyle{\sum_{i=1}^{n}}\lambda_i\right)y=\displaystyle{\sum_{i=1}^{n}}\lambda_ix_i\), on pose \(\mu=\displaystyle{\sum_{i=1}^{n}}\lambda_i\). On a alors : \(f\left(\displaystyle{\sum_{i=1}^{n+1}}\lambda_ix_i\right)=f(\mu y+\lambda_{n+1}x_{n+1})\le\mu f(y)+\lambda_{n+1}f(x_{n+1})\)
en raison de la propriété à l’ordre 2 ; d’autre part , d’après l’hypothèse de récurrence, \(f(y)=f\left(\displaystyle{\sum_{i=1}^{n}}\frac{\lambda_i}\mu x_i\right)\le\displaystyle{\sum_{i=1}^{n}}\frac{\lambda_i}\mu f(x_i)\).
On obtient donc \(f\left(\displaystyle{\sum_{i=1}^{n+1}}\lambda_ix_i\right)\le\displaystyle{\sum_{i=1}^{n+1}}\lambda_if(x_i)\).
Remarque :
Pour établir la récurrence, il suffit de vérifier que la propriété est vraie au départ pour \(n = 1\), mais dans le passage du rang \(n\) au rang \(n+1\), on utilise le fait que la propriété est vraie pour \(n = 2\).