Convexité et taux d'accroissement
Théorème :
Soit \(f\) une application d'un intervalle\( \mathcal I\) dans \(\mathbf R\) ; on note
\(\displaystyle{r_a :\mathcal I/\{a\}\to\mathbf R\quad x\mapsto\frac{f(x)-f(a)}{x-a}}\)
la fonction taux d'accroissement en \(a\) ; \(f\) est convexe si et seulement si , pour tout \(a\in\mathcal I\), la fonction \(r_a\) est croissante sur \(\mathcal I/a\).
Preuve :
Il faut envisager différents cas suivant les positions respectives de \(x_1 , x_2\) et \(a\).
Condition nécessaire
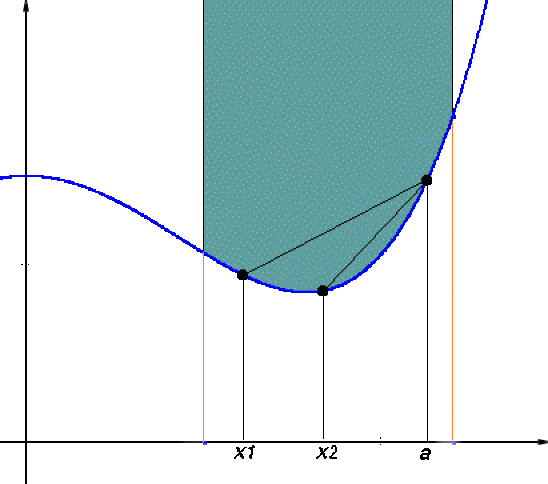
Soit \(f\) convexe sur \(\mathcal I\) ; on considère des points \(\displaystyle{x_1\in\mathcal I/\{a\},x_2\in\mathcal I/\{a\}}\) et on suppose \(x_1< x_2\); on cherche à montrer que \(r_a(x_1)\leq r_a(x_2)\).
On se place dans le cas \(x_1< x_2< a\); on a donc , d'où
\(\displaystyle{x_2=\lambda x_1+(1-\lambda)}\) avec\( \displaystyle{\lambda=\frac{a-x_2}{a-x_1}\in]0,1[}\).
L'hypothèse de convexité de \(f\) entraîne alors :
\(\displaystyle{f(x_2)\leq\frac{a-x_2}{a-x_1}f(x_1)+\frac{x_2-x_1}{a-x_1}f(a)}\)
soit encore, comme \(a> x_1\) :
\((a-x_1)(f(x_2-f(a))\leq(a-x_2)(f(x_1-f(a)))\)
On a donc finalement :
\(\displaystyle{\frac{f(x_1)-f(a)}{x_1-a}\leq\frac{f(x_2)-f(a)}{x_2-a}}\).
Les autres dispositions relatives de \(a, x_1\) et \(x_2\) se traitent de la même façon.
Condition suffisante
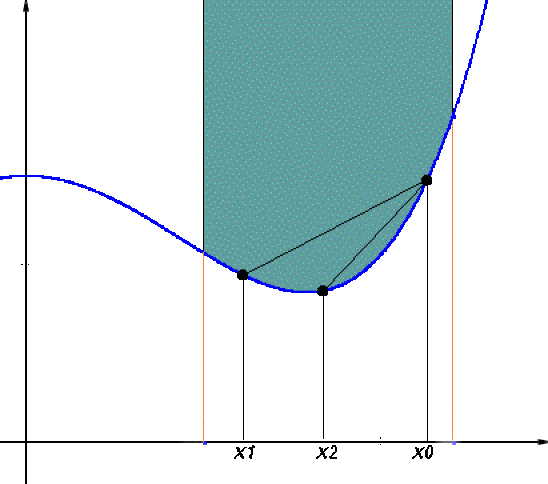
On suppose que, pour tout point \(x_0\) de \(\mathcal I\) la fonction\( r_{x_0}\) est croissante : on considère des points \(x_1\) et \(x_2\) de \(\mathcal I\) avec \(x_1< x_2\); pour\( \lambda\in[0,1[\) on a :
\(x_1<\lambda x_1+(1-\lambda)x_2\leq x_2\).
La croissance de la fonction\( r_{x_1}\) entraîne :
\(\displaystyle{\frac{f(\lambda x_1+(1-\lambda)x_2)-f(x_1)}{(1-\lambda)(x_2-x_1)}\leq\frac{f(x_2)-f(x_1)}{x_2-x_1}}\).
On a \(1-\lambda>0\) et \(x_2-x_1>0\), on en déduit :
\(\displaystyle{f(\lambda x_1+(1-\lambda)x_2)-f(x_1)\leq(1-\lambda)(f(x_2)-f(x_1))}\)
soit
\(\displaystyle{f(\lambda x_1+(1-\lambda)x_2)\leq\lambda f(x_1)+(1-\lambda)f(x_2)}\).
Pour \(\lambda=1\) l'égalité est évidente ; \(f\) est donc convexe sur \(\mathcal I\).
Théorème :
Soit \(f\) une fonction convexe sur un intervalle \(\mathcal I\) de \(\mathbf R\). Alors\( f\) est dérivable à droite et à gauche et donc continue en tout point intérieur à \(\mathcal I\).
Preuve :
C'est une application du théorème précédent.
Soit \(a\) un point intérieur à \(I\) et soient \(\alpha\) et \(\beta\) des points de \(I\) vérifiant \(\alpha<a<\beta\), la fonction \(r_a\) est croissante sur \(I\) .
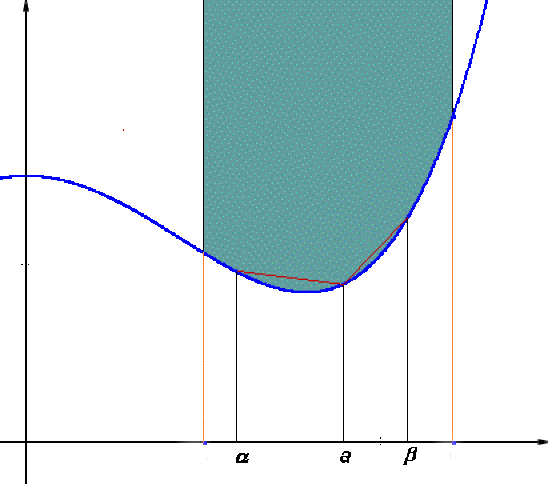
Soit \(x_1\) un point de \(]\alpha,a[\), on a \(\forall x\in]a,\beta[~r_a(\alpha)\le r_a(x_1)\le r_a(x)\le r_a(\beta)\).
Quand \(x\) tend vers \(a\) à droite \(r_a\) croissante et minorée, a une limite et \(f\) est donc dérivable à droite avec : \(r_a(\alpha)\le r_a(x_1)\le f'_a(\alpha)\le r_a(\beta)\).
Soit \(x_2\) un point de \(]\alpha,\beta[\), la fonction \(r_a\) étant croissante sur \([\alpha,a[\) et majorée par \(f'_a(a)\) admet une limite à gauche en \(a\), donc \(f\) est dérivable à gauche en \(a\) et on a : \(r_a(\alpha)\le f'_g(a)\le f'_a(a)\le r_a(\beta)\).
Remarque :
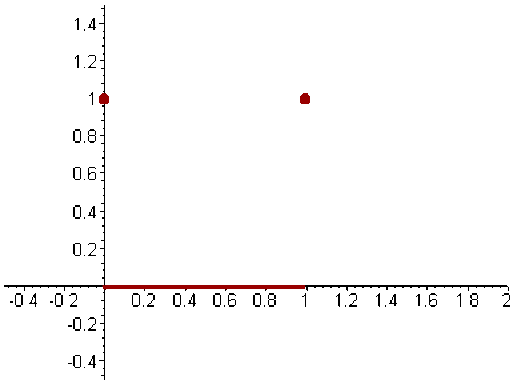
Lorsque \(f\) est convexe sur un intervalle qui n'est pas ouvert elle n'est pas nécessairement continue aux bornes:
Exemple :
Soit\( f :[0,1]\to\mathbf R,\forall x\in]0,1[f(x)=0,f(0)=f(1)=1\)