Exemples d'endomorphismes : homothétie, projection
Homothétie
Soient \(E\) un \(\mathbf K\textrm{-espace-vectoriel}\), et \(k\) un élément de \(\mathbf K\). On définit l'application \(f_k\) par :
\(\left[\begin{array}{rcl} f_k : E &\to& E \\ u &\to& ku \end{array}\right.\)
\(f_k\) est linéaire. En effet, soit \(u\) et \(v\) deux vecteurs de \(E\), \(\alpha\) et \(\beta\) deux scalaires de \(\mathbf K\).
\(\begin{array}{rcll}f_k (\alpha u + \beta v) &=& k(\alpha u + \beta v) &(\textrm{d\'efinition de }f_k)\\&=& k(\alpha u) + k (\beta v)& (\textrm{propri\'et\'e des lois de l'espace vectoriel }E)\\&=& (k \alpha)u + (k \beta)v &(\textrm{propri\'et\'e des lois de l'espace vectoriel }E)\\&=& \alpha (ku) + \beta (kv) &(\textrm{propri\'et\'e des lois de l'espace vectoriel }E)\\&=& \alpha f_k (u) + \beta f_k(v) &(\textrm{d\'efinition de }f_k)\end{array}\)
Si \(k = 0\), \(f_k\) est appelée l'application nulle de \(E\).
Si \(k \ne 0\), \(f_k\) est appelée homothétie de rapport k et si \(k = 1\), \(f_k\) est l'application identique de \(E\).
Si \(k \ne 0\), \(f_k\) est une bijection de \(E\) sur \(E\) (tout élément \(v\) de \(E\) admet un antécédent unique \(u = \frac{1}{k}v\) ) donc c'est un automorphisme de \(E\).
Pour tout réel \(k\) non nul, l'homothétie de rapport k commute avec tout endomorphisme de \(E\), c'est-à-dire, pour tout endomorphisme \(g\) de \(E\),\( h_k \circ g = g \circ h_k\).
En effet, pour tout vecteur \(u\) de \(E\), \(h_k \circ g(u) = kg(u) = g(ku) = g \circ h_k(u)\) (la deuxième égalité est vraie car \(g\) est linéaire).
Projection
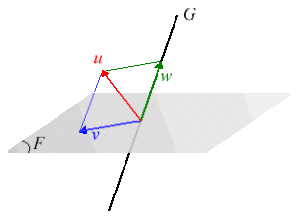
Soient \(E\) un \(\mathbf K\textrm{-espace-vectoriel}\) et \(F\) et \(G\) deux sous-espaces vectoriels supplémentaires dans \(E\).
Tout vecteur \(u\) de \(E\) s'écrit de façon unique \(u = v + w\) avec v élément de \(F\) et \(w\) élément de \(G\).
L'unicité de la décomposition précédente permet de définir l'application \(p\) de\( E\) dans \(E\) telle que \(p(u) = v\).
\(p\) est appelée projection sur \(F\) parallèlement à \(G\).
C'est une application linéaire.
En effet, soient deux vecteurs \(u\) et \(u'\) de \(E\), \(\alpha\) et \(\beta\) deux scalaires de \(\mathbf K\), le vecteur u s'écrit de façon unique \(u = v + w\) avec \(v\) élément de \(F\) et \(w\) élément de \(G\) et, par définition de\( p\), \(p(u) = v\).
Le vecteur \(u'\) s'écrit de façon unique \(u' = v' + w'\) avec v' élément de \(F\) et\( w'\) élément de \(G\) et, par définition de \(p\), \(p(u') = v'\).
\(\alpha u + \beta u' = \alpha (v + w) + \beta (v' + w') = (\alpha v + \beta v') + (\alpha w + \beta w')\)
\(F\) est un sous-espace vectoriel de \(E\), il est donc stable par combinaison linéaire et donc le vecteur \(\alpha v + \beta v'\) appartient à \(F\).
De même le vecteur \(\alpha w + \beta w'\) appartient à \(G\) et, d'après la définition de \(p\),
\(p(\alpha u + \beta u') = \alpha v + \beta v' = \alpha p(u) + \beta p (u')\).
Une projection \(p\) vérifie l'égalité \(p^2 = p\). En effet, soit \(p\) la projection sur \(F\) parallèlement à \(G\), tout vecteur \(u\) de \(E\) s'écrit de façon unique \(u = v + w\) avec v élément de \(F\) et \(w\) élément de \(G\), on a alors \(p(u) = v\) et \(p(v) = v\) car \(v = v + 0\) avec \(v\) élément de \(F\) et 0 élément de \(G\).
Ainsi \(p^2(u) = p \circ p(u) = p(p(u)) = p(v) = v = p(u)\).