Etude d'un endomorphisme involutif de E
Partie
Question
Soient \(E\) un espace vectoriel sur \(\mathbb K\), \(F_1\) et \(F_2\) deux sous-espaces vectoriels supplémentaires de \(E\). On définit l'application \(s\) de \(E\) dans \(E\) de la façon suivante :
Pour tout vecteur \(u\) de \(E\),
il existe un couple unique \((u_1,u_2)\) appartenant à \(F_1\times F_2\) tel que \(u=u_1+u_2\);
l'image de \(u\) par \(s\) est \(s(u)=u_1-u_2\).
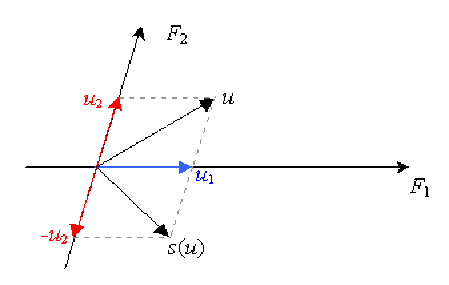
Faire un dessin en prenant pour \(E\) l'espace vectoriel des vecteurs du plan et pour \(F_1\) et \(F_2\) deux droites vectorielles distinctes. De quelle transformation géométrique s'agit-il ?
Montrer que \(s\) est une application linéaire.
Déterminer \(s\circ s\), en déduire que \(s\) est bijective.
Aide simple
Se donner deux scalaires \(\alpha,\beta\) et \(u, v\) deux vecteurs de \(E\).
Décomposer \(u\) et \(v\) en somme d'un vecteur de \(F_1\) et d'un vecteur de \(F_2\) et en déduire la décomposition de \(\alpha u+\beta v\).
Puis comparer \(s(\alpha u+\beta v)\) et \(\alpha s(u)+\beta s(v)\).
Aide méthodologique
Soit une application \(f\) d'un \(\mathbb K\textrm{-espace}\) vectoriel \(E\) dans un \(\mathbb K\textrm{-espace}\) vectoriel \(F\).
Pour démontrer que \(f\) est linéaire, on peut vérifier que :
\(\forall(u,v)\in E^2,f(u+v)=f(u)+f(v)\) et \(\forall(\alpha,u)\in\mathbb K\times E,f(\alpha,u)=\alpha f(u)\)
ou bien que \(\forall(u,v)\in E^2,\forall(\alpha,\beta)\in\mathbb K^2,f(\alpha u,\beta v)=\alpha f(u)+\beta f(v)\).
Aide à la lecture
Deux sous-espaces vectoriels \(F_1\) et \(F_2\) sont supplémentaires si et seulement si leur somme est directe (\(F_1\cap F_2=\{0_E\}\)) et égale à \(E\). Cette définition est équivalente à la propriété :
Tout élément de \(E\) s'écrit, de manière unique, comme somme d'un élément de \(F_1\) et d'un élément de \(F_2\).
Solution détaillée
1. L'application \(f\) est la symétrie par rapport à la droite de direction la droite .
2. Soient \(\alpha,\beta\) deux scalaires et \(u, v\) deux vecteurs de \(E\) ; les sous-espaces \(F_1\) et \(F_2\) étant supplémentaires, \(u\) et \(v\) se décomposent de manière unique comme somme d'un vecteur de \(F_1\) et d'un vecteur de \(F_2\): \(u=u_1+u_2\) et \(v=v_1+v_2\).
D'où \(\alpha u+\beta v=(\alpha u_1+\beta v_1)+(\alpha u_2+\beta v_2)\).
\(\alpha u_1+\beta v_1\in F_1\) et \(\alpha u_2+\beta v_2\in F_2\) car ce sont des sous-espaces vectoriels de \(E\).On compare \(s(\alpha u+\beta v)\) et \(\alpha s(u)+\beta s(v)\):
\(\begin{array}{rcl}s(\alpha u+\beta v)&=&(\alpha u_1+\beta v_1)-(\alpha u_2+\beta v_2)\\&=&\alpha(u_1-u_2)+\beta(v_1+v_2)\\&=&\alpha s(u)+\beta s(v)\end{array}\)
L'application est donc linéaire.
Remarque :
On pouvait aussi montrer que si on appelle \(p_1\) la projection sur \(F_1\) parallèlement à \(F_2\) et \(p_2\) la projection sur \(F_2\) parallèlement à \(F_1\), on a \(s=p_1-p_2\). Or \(p_1\) et \(p_2\) sont des applications linéaires (voir la ressource de cours) donc \(s\) est linéaire.
3. Soit \(u\) un vecteur de \(E\). Il s'écrit de manière unique comme somme d'un vecteur de \(F_1\) et d'un vecteur de \(F_2\): \(u=u_1+u_2\). On calcule \(s\circ s(u)\):
\(s\circ s(u)=s(u_1-u_2)=u_1+u_2=u\)
D'où\(s\circ s=Id_E\).
L'égalité \(s\circ s=Id_E\) montre que \(s\) admet une application réciproque (\(s^{-1}=s\)) ; l'application \(s\) est donc bijective et sa bijection réciproque est \(s\) (on dit que \(s\) est involutive).