Intersection et somme de sous-espaces de R3
Partie
Question
Soit \(F\) l'ensemble des triplets de nombres réels \((x,y,z)\) tels que \(x+y-z=0\).
Montrer que \(F\) est un espace vectoriel et donner sa dimension.
Aide simple
On pourra montrer que \(F\) est l'ensemble des combinaisons linéaires de \(2\) vecteurs.
Solution détaillée
Remarque :
Le choix fait dans cette solution est de ne pas utiliser la notion d'application linéaire. Il est clair que certaines des solutions proposées (en particulier la justification des deux premières questions) peuvent être remplacées par des démonstrations éventuellement plus élégantes mais moins élémentaires faisant intervenir la notion d'application linéaire et les propriétés qui en découlent.
Solution de la question 1. :
La première remarque que l'on peut faire est que \(F\) est une partie de \(\mathbb R^3\). Donc pour démontrer que \(F\) est un espace vectoriel, il suffit donc de démontrer que c'est un sous-espace vectoriel de \(\mathbb R^3\).
Remarquons de plus que \(\mathbb R^3\) étant un espace vectoriel de type fini, tout sous-espace de \(\mathbb R^3\) en sera un aussi ce qui justifie la fin de la question.
Enfin, dernière remarque sur la stratégie que nous allons utiliser : compte tenu de l'ensemble des deux parties de la question, on va essayer de montrer que \(F\) est un sous-espace de \(\mathbb R^3\) en montrant que c'est l'ensemble des combinaisons linéaires de vecteurs de \(\mathbb R^3\), ce qui nous avancera pour la recherche de la dimension, plutôt que d'utiliser la caractérisation des sous-espaces par la stabilité pour les lois puisque de toute façon il faudra chercher un système de générateurs pour avoir la dimension.
Soit donc un élément \(v\) de \(F\). Alors \(v=(x,y,z)\) avec \(x, y,\) et \(z\) réels tels que \(x+y-z=0\).
Cette dernière égalité est équivalente à \(z=x+y\).
Donc \(v\) appartient à \(F\) si et seulement si \(v=(x,y,x+y)\), soit \(v=x(1,0,1)+y(0,1,1)\).
Si l'on appelle \(\epsilon_1\) et \(\epsilon_2\) les vecteurs \((1,0,1)\) et \((0,1,1)\) de \(\mathbb R^3\), on a montré que \(F\) est l'ensemble des combinaisons linéaires à coefficients réels des vecteurs \(\epsilon_1\) et \(\epsilon_2\). Ceci prouve que \(F\) est un sous-espace vectoriel de \(\mathbb R^3\).
De plus on a une famille génératrice de \(F\). Comme il est clair que les vecteurs \(\epsilon_1\) et \(\epsilon_2\) ne sont pas proportionnels, ils sont linéairement indépendants.
Donc \((\epsilon_1,\epsilon_2)\) est une base de \(F\) qui est donc de dimension égale à \(2\).
Question
Soit \(G\) l'ensemble des triplets de nombres réels \((x,y,z)\) tels que \(x=y\).
Montrer que \(G\) est un sous-espace vectoriel de \(\mathbb R^3\) et donner sa dimension.
Solution détaillée
La méthode utilisée est la même que dans la question précédente, pour les mêmes raisons.
Soit donc un élément \(v\) de \(G\). Alors \(v=(x,y,z)\) avec \(x, y,\) et \(z\) réels tels que \(x=y\).
Donc \(v\) appartient à \(G\) si et seulement si \(v=(x,x,z)\), soit \(v=x(1,1,0)+z(0,0,1)\).
Si l'on appelle \(w_1\) et \(w_2\) les vecteurs \((1,1,0)\) et \((0,0,1)\) de \(\mathbb R^3\), on a montré que \(G\) est l'ensemble des combinaisons linéaires à coefficients réels des vecteurs \(w_1\) et \(w_2\).
Ceci prouve que \(G\) est un sous-espace vectoriel de \(\mathbb R^3\).
De plus on a une famille génératrice de \(G\). Comme il est clair que les vecteurs \(w_1\) et \(w_2\) ne sont pas proportionnels, ils sont linéairement indépendants.
Donc \((w_1,w_2)\) est une base de \(G\) qui est donc de dimension égale à \(2\).
Question
Trouver une base de l'intersection \(F\cap G\) et donner sa dimension.
Solution détaillée
Le plus simple pour répondre à cette question est d'utiliser la définition de chacun des sous-espaces \(F\) et \(G\). Soit donc un élément \(v\) de \(F\cap G\).
Alors \(v=(x,y,z)\) avec \(x, y,\) et \(z\) réels tels que \(z=x+y\) et \(x=y\).
Relations équivalentes aux relations \(z=2y\) et \(x=y\).
Donc \(v\) appartient à \(F\cap G\) si et seulement si \(v=(y,y,2y)=y(1,1,2)\). Le vecteur non nul \((1,1,2)\) engendre \(F\cap G\).
Il définit donc une base de \(F\cap G\) qui est donc de dimension égale à \(1\).
Question
On identifie \(\mathbb R^3\) à l'espace de la géométrie usuelle, muni d'un repère \((O, A, B, C)\).
Dessiner l'ensemble \(P\) des triplets \((x,y,0)\).
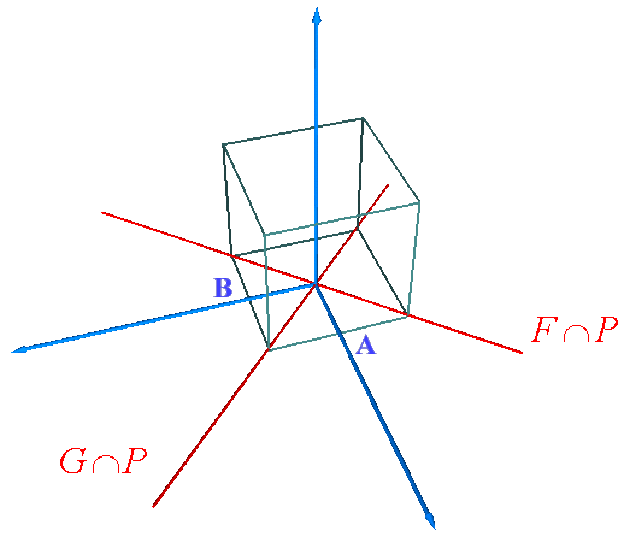
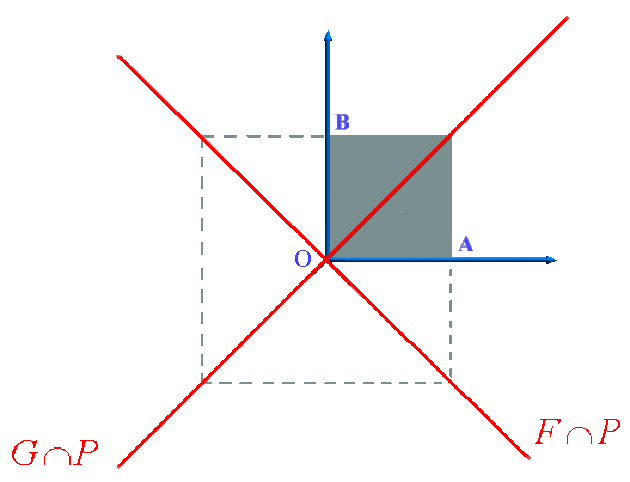
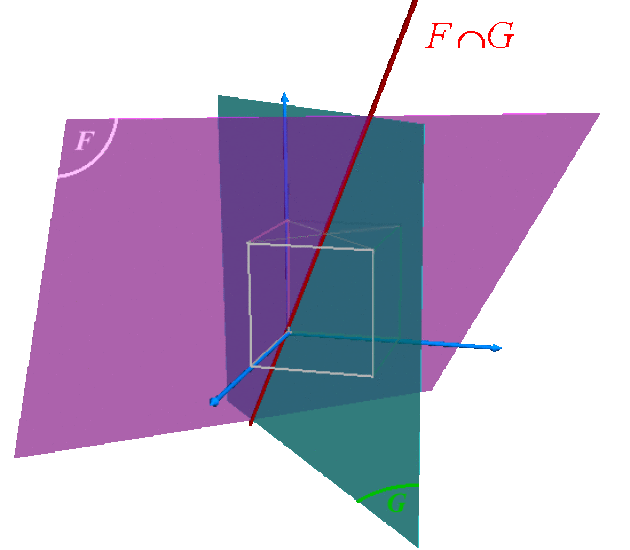
Dessiner \(F\cap P\), \(G\cap P\) et \(F\cap G\).
Caractériser géométriquement \(F\) et \(G\).
Solution détaillée
Ensemble \(P\) des triplets \((x,y,0)\)
\(F\cap P\) et \(G\cap P\)
\(F\cap P\) et \(G\cap P\) dans le plan \(P\)
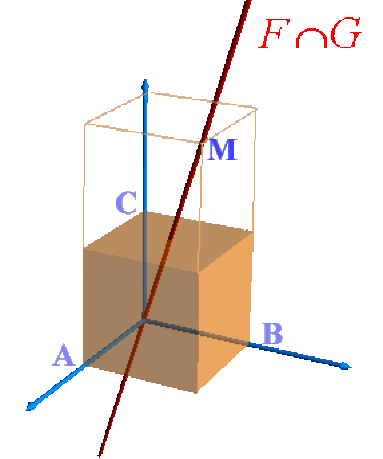
\(F\cap P\)
\(F\cap P\)
Les sous-espaces \(F\) et \(G\) sont des plans vectoriels dans \(\mathbb R^3\).
Comme \(\mathbb R^3\) est de dimension \(3\) et que chacun d'eux est de dimension \(2\) \((=3-1)\), ce sont des hyperplans en utilisant la terminologie générale des espaces vectoriels de type fini.
Question
Trouver un vecteur de \(F\) et un vecteur de \(G\) dont la somme dans \(\mathbb R^3\) n'appartient pas
à la réunion \(F\cup G\).
Solution détaillée
Prenons par exemple \(\epsilon_1\) et \(w_1\).
On a :\(\epsilon_1+w_1=(1,0,1)+(1,1,0)=(2,1,1)\). Les composantes du vecteur \((2,1,1)\) ne vérifient ni la propriété caractéristique des éléments de \(F\): \(z=x+y (1\neq2+1)\) ni celle des éléments de \(G\) : \(x=y\) \((1\neq 2)\).
Donc le vecteur \(\epsilon_1+w_1=(2,1,1)\) n'appartient ni à \(F\) ni à \(G\) et donc n'appartient pas à \(F\cup G\).
Question
Montrer que \(\mathbb R^3\) est égal à la somme \(F+G\).
Justifier que la somme \(F+G\) n'est pas directe.
Solution détaillée
Nous savons que la somme \(F+G\) est un sous-espace vectoriel de \(\mathbb R^3\).
Compte tenu du résultat de la \(3^{\circ}\) question, le sous-espace \(F\cap G\) n'est pas réduit au vecteur nul, donc la somme \(F+G\) n'est pas directe.
Nous allons indiquer deux méthodes possibles pour montrer que \(\mathbb R^3=F+G\).
La première, élémentaire, consiste à démontrer l'inclusion \(\mathbb R^3\subset F+G\) en utilisant la définition de la somme de sous-espaces.
Soit donc \(u=(x,y,z)\) un élément quelconque de \(\mathbb R^3\).
Pour démontrer l'inclusion \(\mathbb R^3\subset F+G\), il faut montrer l'existence d'un élément \(u'=(x',y',z')\) de \(F\) et d'un élément \(u''=(x'',y'',z'')\) de \(G\) tels que \(u=u'+u''\).
L'élément \(u'=(x',y',z')\) appartient à \(F\) si et seulement si il s'écrit \(u'=(x',y',x'+y')\).
L'élément \(u''=(x'',y'',z'')\) appartient à \(G\) si et seulement si il s'écrit \(u''=(x'',y'',z'')\).
Il s'agit donc de montrer que le système réel suivant a au moins une solution :
\(\left\{\begin{array}{rcrcrcrcr} x'&+&x''&&&&&=&x \\ &&x''&+&y'&&&=&y \\ x'&+&&&y'&+&z''&=&z \end{array} \right.\)
où \((x',y',x'',z'')\) représentent l'inconnue et \(x, y, z\) les données.
Ce système est équivalent au système :
\(\left\{\begin{array}{rcrcrcrcc} x'&+&x''&&&&&=&x \\ &&x''&+&y'&&&=&y \\ &-&x''&+&y'&+&z''&=&z-x \end{array} \right.\)
qui est lui-même équivalent à
\(\left\{\begin{array}{rcrcrcrcc} x'&+&x''&&&&&=&x \\ &&x''&+&y'&&&=&y \\ &&&&2y'&+&z''&=&z-x+y \end{array} \right.\)
D'où on déduit qu'un quadruplet \(\left(\frac{1}{2}(x+z-y-z''), \frac{1}{2}(-x+z+y-z''), \frac{1}{2}(x-z+y-z'')\right)\) où \(z''\) est un réel quelconque est solution du système. Notez qu'il n'y a pas unicité des solutions (résultat attendu puisque la somme n'est pas directe).
La deuxième méthode, utilisant la notion de dimension, consiste à démontrer \(\mathbb R^3\) que \(F+G\) et ont même dimension.
Elle est basée sur la propriété du cours suivante : si \(E_1\) et \(E_2\) sont deux sous-espaces vectoriels d'un espace vectoriel \(E\) de type fini, on a :
\(\dim(E_1+E_2)=\dim E_1 + \dim E_2 - \dim(E_1 \cap E_2)\).
En appliquant ce résultat, ici, compte tenu des résultats des trois premières questions, on obtient :
\(\dim(F+G)=2+2-1=3\)
Le sous-espace \(F+G\), inclus dans \(\mathbb R^3\) et ayant même dimension que \(\mathbb R^3\), est donc égal à \(\mathbb R^3\).
Question
Trouver un sous-espace \(F'\) de \(\mathbb R^3\) tel que la somme \(F+F'\) soit directe.
Aide simple
De quelle dimension sera nécessairement \(F'\)?
Solution détaillée
Pour répondre à la question, il suffit de trouver un vecteur \(v\) de \(\mathbb R^3\) tel que \(\{v,\epsilon_1,\epsilon_2 \}\) soit une partie libre (un tel vecteur existe d'après le théorème de la base incomplète appliqué à la famille libre \(\{\epsilon_1,\epsilon_2 \}\)).
Le sous-espace de \(\mathbb R^3\) engendré par un tel vecteur répondra à la question.
Il y a donc une infinité de solution.
Par exemple considérons le premier vecteur de la base canonique de \(\mathbb R^3\), \(e_1=(1,0,0)\).
Soit \(\alpha, \beta, \gamma\) des scalaires tels que \(\alpha e_1+ \beta\epsilon_1+\gamma\epsilon_2=0\).
Cette égalité équivaut à l'égalité : \((\alpha+\beta,\gamma,\beta+\gamma)=(0,0,0)\), qui implique immédiatement \(\alpha=\beta=\gamma=0\).
La famille \(\{e_1,\epsilon_1,\epsilon_2\}\) est donc libre et le sous-espace \(F'=\mathbb Re_1\) est bien tel que la somme \(F+F'\) soit directe.
Remarquons que la simple considération des dimensions prouve que tout sous-espace répondant à la question sera un supplémentaire de \(F\) (i.e. tel que \(F\oplus F'=\mathbb R^3\)).
Question
Quelles sont les dimensions possibles des sous-espaces vectoriels de \(\mathbb R^3\)?
Donner un exemple de chaque.
Solution détaillée
On sait que la dimension d'un espace vectoriel est un entier positif ou nul, et que la dimension d'un sous-espace d'un espace de type fini est inférieure à la dimension de l'espace.
Alors, comme la dimension de \(\mathbb R^3\) est égale à \(3\), les dimensions possibles des sous-espaces vectoriels de \(\mathbb R^3\) sont \(0, 1, 2\) et \(3\).
Il existe bien des sous-espaces de \(\mathbb R^3\) ayant ces dimensions.
En effet tout d'abord les sous-espaces "triviaux" : \(\{0\}\) est le seul sous-espace de dimension \(0\) et \(\mathbb R^3\) est le seul sous-espace de dimension \(3\).
Pour les autres dimensions possibles il n'y a évidemment pas unicité, \(F'=\mathbb Re_1\) est un espace de dimension \(1\) et \(F\) est un espace de dimension \(2\).
Question
Montrer que, quelque soient \(P\) et \(Q\) deux plans de \(\mathbb R^3\) (i.e. deux sous-espaces vectoriels de \(\mathbb R^3\) de dimension \(2\)), \(P\cap Q\neq \{0\}\).
Solution détaillée
Une démonstration par l'absurde donne immédiatement le résultat.
En effet soient \(P\) et \(Q\) deux sous-espaces de \(\mathbb R^3\) de dimension \(2\). Si \(P\cap Q=\{0\}\), la somme des sous-espaces \(P\) et \(Q\) est directe et l'on a
\(\dim (P\oplus Q)=\dim P+\dim Q=2+2=4\).
Or \(P \oplus Q\) est un sous-espace de \(\mathbb R^3\) qui est de dimension \(3\), on a donc une absurdité.
Question
Soient \(D\) et \(\Delta\) deux droites de \(\mathbb R^3\)(i.e. deux sous-espaces vectoriels de \(\mathbb R^3\) de dimension \(1\)).
Montrer que soit \(D\cap \Delta= \{0\}\), soit \(D\cap \Delta=D=\Delta\).
Solution détaillée
On sait que l'intersection de deux sous-espaces vectoriels est un sous-espace vectoriel.
Comme \(D\cap\Delta\) est inclus dans \(D\) et dans \(\Delta\), est un sous-espace vectoriel de \(D\) et un sous-espace vectoriel de \(\Delta\).
Comme \(D\) et \(\Delta\) sont de dimension \(1\), leurs sous-espaces ne peuvent être que de dimension \(0\) ou \(1\).
Si \(D\cap \Delta\) est différent de \(\{0\}\), sa dimension n'est pas égale à \(0\) et donc elle vaut \(1\).
Or on sait que si deux sous-espaces vectoriels sont inclus l'un dans l'autre et si ils ont même dimension, ils sont égaux.
On en déduit donc que \(D\cap\Delta=D\) et \(D\cap\Delta=\Delta\).
On trouve donc le résultat "naturel" suivant : deux droites vectorielles sont ou confondues, ou n'ont en commun que le vecteur nul (ne pas oublier que toutes les droites vectorielles contiennent \(0\)).