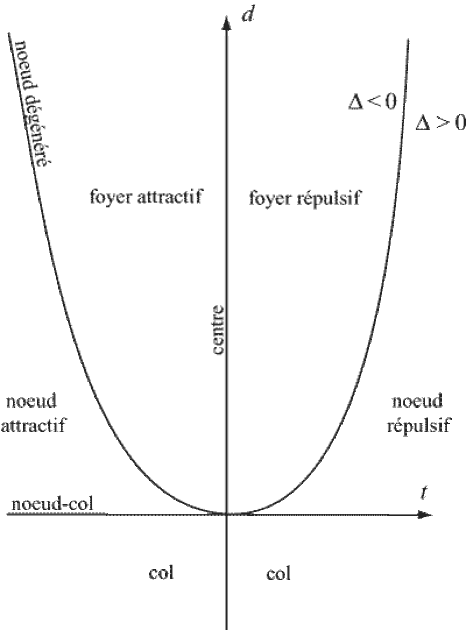
Diagramme de bifurcations
Soit \(\displaystyle{\left\{\begin{array}{ll}x'=f(x,y) \\ y'=g(x,y)\end{array}\right.}\)
un système de deux équations linéaires, qu'on peut aussi écrire
\(X' = A X\), où A est la matrice \(\displaystyle{\left(\begin{array}{cc}a&b \\c&d\end{array}\right)}\)
On a déjà étudié la nature du point stationnaire situé à l'origine suivant la valeur des valeurs propres \(\lambda_1\), \(\lambda_2\) de la matrice A :
si \(\lambda_1\), \(\lambda_2\) sont réelles de même signe, on a un nœud, qui est :
attractif si elles sont négatives,
répulsif si elles sont positives.
si \(\lambda_1\), \(\lambda_2\) sont réelles de signe contraire, on a un col .
si \(\lambda_1\), \(\lambda_2\) sont complexes conjuguées, on a
un foyer attractif si elles sont de partie réelle négative,
un centre si elles sont imaginaires pures,
un foyer répulsif si elles sont de partie réelle positive.
Ces conditions peuvent en fait s'exprimer en fonction de la somme et du produit de ces valeurs propres, qui ne sont autres que la trace et le déterminant de la matrice A, c'est à dire \(\textrm{tr}(A)=a+d\) et \(\textrm{det}(A) = ad - bc\).
Les valeurs propres \(\lambda_1\), \(\lambda_2\) sont les racines du polynôme caractéristique \(\lambda^2 - \textrm{tr}(A)\lambda + \textrm{det}(A)\).
Notons \(\Delta = \textrm{tr}(A)^2 - 4\textrm{det}(A)\) le discriminant de ce polynôme.
La classification suivant la nature du point stationnaire s'exprime alors comme suit :
1. Si \(\Delta > 0\) (valeurs propres réelles), alors :
si \(\textrm{det}(A) > 0\), on a un nœud, qui est
attractif si \(\textrm{tr}(A) < 0\),
répulsif si \(\textrm{tr}(A) < 0\) ;
si \(\textrm{det}(A) < 0\), on a un col.
2. Si \(\Delta < 0\)(valeurs propres complexes conjuguées), alors :
si \(\textrm{tr}(A) < 0\), on a un foyer attractif,
si \(\textrm{tr}(A) = 0\) (valeurs propres imaginaires pures) on a un centre,
si \(\), on a un foyer répulsif.
On peut visualiser les résultats ci-dessus dans le plan \((t,d) = (\textrm{tr}(A), \textrm{det}(A))\), comme dans la figure suivante, où les axes et la parabole d'équation \(d = t^2/4\) (c'est à dire \(\delta=0\)) délimitent des régions correspondant aux différents cas ci-dessus.
Allez voir les animations suivantes, qui concernent des systèmes linéaires dépendants d'un paramètre \(p\). Vous y verrez simultanément, pour chaque valeur de \(p\), l'allure du portrait de phase et la position du point \(M = (\textrm{tr}(A), \textrm{det}(A))\) dans le plan \((t, d)\). Lorsque le point M change de région, l'allure du portrait de phase change, parfois de façon assez brusque. Ce phénomène porte le nom de bifurcation.