Oscillations
Partie
Question
Ressort pendu dans l'air et dans l'huile (*)
On suspend une bille de masse m à un ressort souple de longueur à vide \(\displaystyle{l_0}\) qui s'allonge de ce fait d'une longueur\( \displaystyle{\Delta l}\) .
Quelle est la constante de raideur \(k\) du ressort, si \(\Delta l= 49 \textrm{ mm}\) pour \(m = 20 \textrm{ g}\)? On prendra pour l'accélération de la pesanteur \(g = 9,8 \textrm{ ms}^{-2}\).
On écarte la bille vers le bas de la même longueur \(\Delta l\) et on l'abandonne sans vitesse initiale. Ecrire l'équation du mouvement. Calculer la période des oscillations (on garde les valeurs numériques du 1°).
Aide simple
néant
Solution détaillée
1) -- A l'équilibre, la masse est soumise à son poids et à la force de tension du ressort :
\(\displaystyle{\overrightarrow T=-k(l_0+\Delta l)\overrightarrow i=\overrightarrow P=mg\overrightarrow i}\)
On trouve avec les valeurs numériques de l'énoncé, \(k = 4 \textrm{ N.m}^{-1}\).
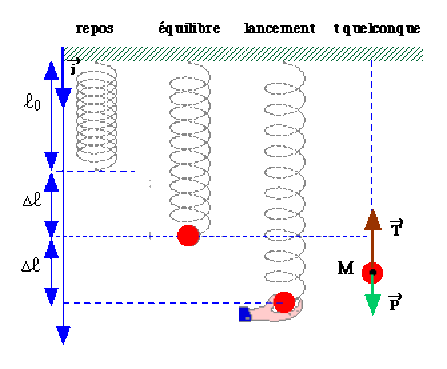
2) -- On écarte la bille de \(\Delta l\) de sa position d'équilibre et on l'abandonne sans vitesse initiale. L'équation du mouvement s'obtient en appliquant le principe fondamental:
\(\displaystyle{\overrightarrow T+\overrightarrow P=m\overrightarrow a\textrm{ avec }\overrightarrow T=-k(l_0+\Delta l+x)\overrightarrow i\textrm{ et }\overrightarrow P=mg\overrightarrow i}\)
d'où
\(\displaystyle{x"+\frac{k}{m}x=0}\)
La solution est sinusoïdale: la masse oscille autour de la position\( \displaystyle{l_0=\Delta l}\) .
La période est \(\displaystyle{T_0=\frac{2\pi}{\omega_0}\textrm{ avec }\omega_0^2=\frac{k}{m}}\)
A.N. \(T_0 = 0,444\textrm{ s}\).