Mouvement d'une masse fixée à un ressort en rotation libre autour d'un axe
Partie
Question
Mouvement d'une masse fixée à un ressort en rotation libre autour d'un axe (**)
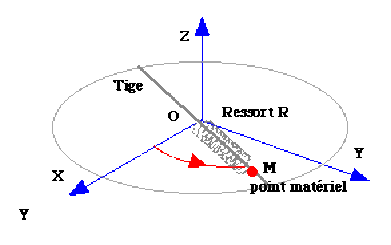
Un point matériel \(M\) de masse \(m\) est assujetti à glisser sans frottement sur une tige horizontale \(OM\). Il est attaché à l'une des extrémités d'un ressort \(R\) de dureté\( K\), dont l'autre extrémité est fixée au point \(O\). La tige \(OM\) tourne librement autour de l'axe vertical \(OZ\). Etudier le mouvement du point \(M\) par rapport au référentiel (\(O, XYZ\)).
On note \(\Omega_0\) la vitesse angulaire initiale donnée à la tige. Les conditions initiales sont : \(\omega_0 > \Omega_0, \rho(0) = \rho_0 \textrm{ et }\rho'(0) = 0\)
Aide simple
Il faut traduire le couplage entre le mouvement de la masse m par rapport à la tige, et le mouvement de rotation de la tige. La tige tourne librement, ce qui implique qu'elle n'est soumise à aucun couple : la seule force exercée sur la tige est centrale. Reprendre les relations de composition des acccélérations. Faire le bilan des forces et décomposer dans la base cylindrique.
Solution détaillée
On définit le référentiel [\(R\)] "relatif" à partir du repère cylindrique : \((O,\overrightarrow u_\rho,\overrightarrow u_\theta ,\overrightarrow k)\) lié à la tige. Le référentiel [\(R_a\)] "absolu" est celui du laboratoire: \((O,\overrightarrow i,\overrightarrow j,\overrightarrow k)\) . Le point matériel \(M\), assujetti à se déplacer sans frottement sur la tige qui l'entraine à vitesse de rotation variable autour de l'axe vertical \(OZ\), est soumis, par rapport au référentiel galiléen lié au laboratoire, à l'accélération
\(\displaystyle{\overrightarrow\gamma_a=\overrightarrow\gamma_r+\overrightarrow\gamma_e+\overrightarrow\gamma_c}\)
\(\displaystyle{\overrightarrow\gamma_r=\rho"\overrightarrow u_\rho}\)
\(\displaystyle{\overrightarrow\gamma_e=\overrightarrow\Omega'\wedge\overrightarrow{OM}+\overrightarrow\Omega\wedge[\overrightarrow\Omega\wedge\overrightarrow{OM}]=\rho\Omega'.\overrightarrow u_\theta-\rho\Omega^2.\overrightarrow u_\rho}\)
\(\overrightarrow\gamma_c=2\overrightarrow\Omega\wedge\overrightarrow V_r=2\rho'\Omega.\overrightarrow u\theta\)
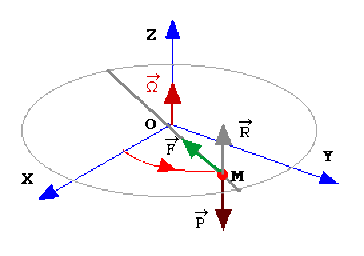
Le point matériel \(M\) est soumis à trois forces : le poids , la réaction \(\overrightarrow R\) du support, la force de tension du ressort \(\displaystyle{\overrightarrow T=K(\rho-l_0)\overrightarrow u_\rho}\) . Le principe fondamental s'écrit sous forme vectorielle :
\(\displaystyle{\overrightarrow P+\overrightarrow R+\overrightarrow T=m\overrightarrow\gamma_a\quad(1)}\)
avec \(\displaystyle{\overrightarrow R=X\overrightarrow u_\rho+Y\overrightarrow u_\theta+Z\overrightarrow k}\) où \(X,Y \textrm{ et }Z\) sont à déterminer a priori. La rotation étant libre, il n'y a pas de composante de \(\overrightarrow R\) selon \(\overrightarrow u_\theta\) , ce qui donne \(Y = 0\). L'absence de frottement entre la tige et le point \(M\), entraine que le travail de la réaction au cours du déplacement relatif (\(M\) sur tige) est identiquement nul :
\(\displaystyle{\overrightarrow R\cdot\overrightarrow{\textrm dM}=0\iff X=0}\)
Le mouvement étant plan, la composante, verticale, de la réaction équilibre le poids. La décomposition de (1) dans la base "relative" conduit aux trois équations ci-après, par suite:
\(\displaystyle{Z-mg=mz"=0\quad(2)}\)
\(\displaystyle{-K(\rho-l_0)=m.(\rho"-\rho\Omega^2)\quad(3)}\)
\(\displaystyle{m\rho\Omega'+m2\rho'\Omega=0\quad(4)}\)
Dans l'équation (3),\( l_0\) est la longueur au repos du ressort et \(\Omega\) varie au cours du temps.
En posant \(\displaystyle{\omega_0^2=\frac{K}{m}}\) , on obtient :
\(\displaystyle{\rho"(t)+\rho(t).[\omega_0^2-\Omega^2(t)]=\omega_0^2l_0\quad(5)}\)
La relation (4) donne la loi des aires : \(\displaystyle{\frac{\textrm d(\rho^2\Omega)}{\textrm dt}=0}\) , soit \(\displaystyle{\rho^2(t).\Omega(t)=\sigma\quad(6)}\) (6)
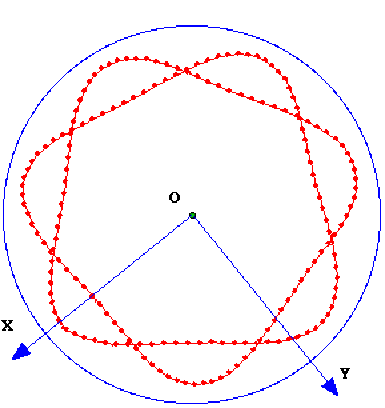
Le moment cinétique \(\sigma\) est constant au cours du mouvement. Dans le cas général, ce système (5) et (6) de deux équations couplées n'est pas aisément intégrable. Le graphe ci-dessous correspond au cas \(\omega_0 = 4 \;\Omega\) d'une solution périodique.
Le système d'équations (5) et (6) peut être résolu selon deux approximations différentes :
A : Approximation d'une vitesse de rotation faible : \(\displaystyle{\omega_0^2\gg\Omega^2(t)}\)
\(\displaystyle{\rho"+\rho\omega_0^2=\omega_0^2l_0}\)
B : Approximation des petites oscillations :
Dans ce cas, on posera
\(\displaystyle{\rho(t)=l_0+u(t)}\)
où\( \displaystyle{\frac{u}{l_0}}\) sera un infiniment petit d'ordre 1.
\(\displaystyle{\rho"+\rho\omega_0^2-\rho\Omega^2=\omega_0^2l_0}\)
\(\displaystyle{\rho\Omega^2=\frac{\sigma^2}{\rho^3}=\frac{\sigma^2}{(l_0+u)^3}\simeq(\frac{\sigma^2}{l_0^3}).(\frac{1-3.u}{l_0})}\)
\(\displaystyle{u"+(\omega_0^2+\frac{3\sigma^2}{l_0^4}).u=\frac{\sigma^2}{l_0^3}}\)
Dans les deux cas, si on pose les conditions initiales suivantes : \(\omega_0 > \Omega_0, \rho(0) = \rho_0 \textrm{ et }\rho'(0) = 0\)
Une solution particulière constante est possible :
\(\displaystyle{\rho=\frac{\omega_0^2l_0}{(\omega_0^2-\Omega_0^2)}}\)
Approximation A: Oscillateur spatial
Une solution particulière de (6) est :\( \displaystyle{\rho_p=l_0}\)
La solution générale de l'équation avec 2° membre nul est : \(\displaystyle{\rho(t)=U.\cos(\omega_0t+\Phi)}\).
Les conditions initiales :
\(\displaystyle{\rho(0)=U.\cos(\Phi)=\rho_0\textrm{ et }\rho'(0)=-\omega.U.\sin(\Phi)=0}\)
autorisent la solution : \(\Phi=0\), d'où\( \displaystyle{\rho(t)=U.\cos(\omega_0t)}\)
La solution générale de l'équation (6) est donc :
\(\displaystyle{\rho(t)=l_0+U.\cos(\omega_0t)}\)
\(\displaystyle{\rho(t)=l_0+(\rho_0-l_0).\cos(\omega_0t)\Rightarrow\Omega(t)=\frac{\sigma}{\rho^2}}\)
a la même période que r(t).
Approximation B : Petites oscillations
On pose dans l'équation (7) :
\(\displaystyle{\omega^2=\frac{\omega_0^2+3\sigma^2}{l_0^4}}\)
Une solution particulière de (7) est :
\(\displaystyle{u_p=\frac{\sigma^2}{(l_0^3.\omega^2)}}\)
La solution générale de l'équation avec 2° membre nul est :
\(u(t)=U.\cos(\omega t+\Phi)\)
La solution générale de l'équation (7) est donc :
\(\displaystyle{u(t)=u_p+U.\cos(\omega t+\Phi)}\)
Les conditions initiales : \(u(0)=u_p+U.\cos(\Phi)=\rho_0\textrm{ et }u'(0)=-\omega.U.\sin(\Phi)=0\)
autorisent la solution :\( \displaystyle{\Phi=0,\textrm{ d'où }\rho(0)=l_0+u(0)=l_0+u_p+U=\rho_0}\)
D'où :
\(\displaystyle{u(t)=u_p+(\rho_0-l_0-u_\rho).\cos(\omega t)}\)
et
\(\displaystyle{\rho(t)\simeq l_0+u_p+(\rho_0-l_0-u_p).\cos(\omega t)}\)
soit encore
\(\begin{array}{rcl}\rho(t)=l_0+u(t)\Rightarrow\Omega(t)&=&\frac{\sigma}{\rho^2}(t)\simeq(\frac{\sigma}{l_0^2}).(\frac{1-2u(t)}{l_0})\\\Rightarrow\Omega(t)&\simeq&(\frac{\sigma}{l_0^2})-2(\frac{\sigma}{l_0^3})[u_p+(\rho_0-l_0-u_p).\cos(\omega t)]\end{array}\)
Dans cette approximation, \(\Omega(t) \textrm{ et }\rho(t)\) ont la même période \(\displaystyle{T=\frac{2\pi}{\omega}}\) .