Mouvement d'une masse fixée à un ressort tournant à vitesse angulaire constante ( suite)
Partie
Question
Mouvement d'une masse fixée à un ressort tournant à vitesse angulaire constante ( suite) (*)
5) -- Quelle est l'équation différentielle qui rend compte du mouvement de \(M\) sur la tige. Résoudre complètement cette équation différentielle ;
a) dans le cas où \(\Omega = \omega_0\)
b) dans le cas où \(\Omega < \omega_0\). On posera alors \(\displaystyle{\omega^2=\omega_0^2-\Omega^2}\) et on appellera\( \rho_p\) la solution particulière de l'équation complète. Exprimer \(\rho_p\).
c) dans le cas où \(\Omega > \omega_0\). On posera alors \(\displaystyle{a^2=\vert\omega_0^2-\Omega^2\vert}\) .
Caractériser la nature des mouvements dans chacun de ces cas?
Aide simple
Utiliser l'intégration des équations différentielles à coefficients constants. Ne pas oublier les conditions initiales.
Solution détaillée
5) L'équation (3) s'écrit
\(\displaystyle{-K(\rho-l_0)=m(\rho"-\rho\Omega^2)}\)
où\( l_0\) est la longueur au repos du ressort.
En posant :\( \displaystyle{\omega_0^2=\frac{K}{m}}\) , on obtient :
\(\displaystyle{\rho"+\rho(\omega_0^2-\Omega^2)=\omega_0^2l_0\quad(5)}\)
Résolution de l'équation (5) ayant pour conditions initiales :
\(\displaystyle{t=0\iff OM_0=\rho_0,\theta_0=0,\rho'=0}\)
On ne traite que le cas\( \rho(t) > 0\).
Plusieurs cas sont possibles :
cas a) \(\displaystyle{\omega_0=\Omega :\Rightarrow\rho"=\omega_0^2l_0}\)
\(\displaystyle{t\to\rho(t)}\) est uniformément accéléré, d'accélération :
\(\displaystyle{\rho"=\omega_0^2l_0}\)
Les conditions initiales donnent :
\(\displaystyle{\rho(t)=\rho_0+(\frac{1}{2})\omega_0^2l_0t^2}\)
cas b et c) \(\displaystyle{\omega_0\neq\Omega}\)
L'équation différentielle est linéaire à coefficients constants; sa solution générale est la somme d'une solution particulière :
\(\displaystyle{\rho_p=\frac{\omega_0^2l_0}{(\omega_0^2-\Omega^2)}}\)
et de la solution générale de l'équation avec second membre nul :
\(\displaystyle{\rho"+\rho(\omega_0^2-\Omega^2)=0}\)
\(\displaystyle{\omega_0>\Omega :t\to\rho(t)}\) est sinusoïdal de pulsation \(\omega\) telle que :
\(\displaystyle{\omega^2=\omega_0^2-\Omega^2}\)
La solution est de la forme
\(\displaystyle{\rho(t)=\rho_p+A\cos(\omega t+\Phi)}\)
En calculant les constantes d'intégration en fonction des conditions initiales, on obtient :
\(\displaystyle{\rho(t)=\rho_p+(\rho_0-\rho_p)}.\cos\omega t\textrm{ et }\theta(t)=\Omega(t)(\rho_0<2\rho_p)\)
On aura une solution [\(\rho(t), \Omega(t)\)] périodique si la période \(\displaystyle{T=\frac{2\pi}{\Omega}}\) de rotation est multiple de la période \(\displaystyle{\tau=\frac{2\pi}{\omega}}\) d'oscillation, donc pour les valeurs entières de \(n> 0\) telles que
\(\displaystyle{\omega=n.\Omega\Rightarrow\omega^2=n^2.\Omega^2\Rightarrow\omega_0^2=(n^2+1).\Omega^2}\)
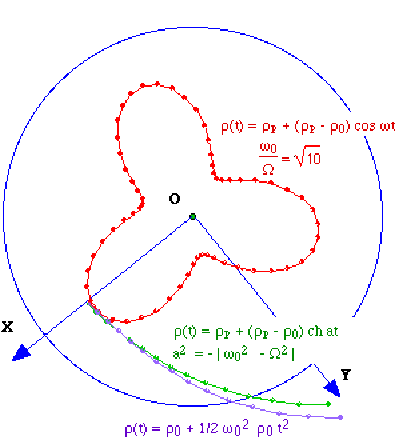
cas c) \(\displaystyle{\omega_0<\Omega :t\to\rho(t)}\) est hyperbolique d'argument at, avec : \(\displaystyle{a^2=\Omega^2-\omega_0^2}\)
L'équation s'écrit \(\displaystyle{\rho"-a^2\rho=\omega_0^2l_0}\)
La solution est de la forme
\(\displaystyle{\rho(t)=\rho_p+A\textrm{ ch }at+B\textrm{ sh }at}\)
En déterminant \(A \textrm{ et }B\) à l'aide des conditions initiales, on obtient :
\(\displaystyle{\rho(t)=\rho_p+(\rho_0-\rho_p).\textrm{ ch }at}\)
et\( \theta(t)=\Omega t \). Cette solution \(\rho(t)\) diverge lorsque \(t\) tend vers l'infini.