Oscillations
Partie
Question
Oscillations sinusoïdales d'une masse sur une tige tournant à vitesse angulaire constante. (*)
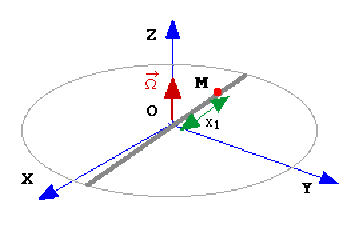
Un point \(M\) est assujetti à se déplacer sur une tige horizontale \(OM\), et il effectue des oscillations sinusoïdales. La tige \(OM\) tourne à vitesse angulaire constante autour de l'axe vertical \(OZ\). Représenter le mouvement du point M par rapport au référentiel ( \(O, XYZ\) ).
Aide simple
Il s'agit d'un problème de cinématique, qui se résoud en composant les vitesses : mouvement "relatif" par rapport à l'axe de la tige, et mouvement "absolu" par rapport au référentiel du laboratoire.
D'autre part, on ne se préoccupe pas de savoir de quelle façon sont obtenus ces mouvements...
Il faut exprimer les variations en fonction du temps de l'angle de rotation et de la distance \(OM\)
Il ne faut pas confondre la pulsation d'un mouvement sinusoïdal et la vitesse de rotation de la tige.
Solution détaillée
Le vecteur rotation instantanée de la tige est noté \(\overrightarrow\Omega\). On pose\( \displaystyle{\overrightarrow{OM}=x_1}\)
Les mouvements se composent selon deux axes orthogonaux liés à la représentation cartésienne "mobile".
Les coordonnées \(x_1\) et \(\theta\) varient en fonction du temps selon les lois :
\(\displaystyle{\theta(t)=\Omega t+\theta_0 ;x_1(t)=A\cos\omega_0t}\)
où \(\omega_0\) est la pulsation du mouvement de la masse sur la tige et \(\Omega\) la vitesse uniforme de rotation de la tige.
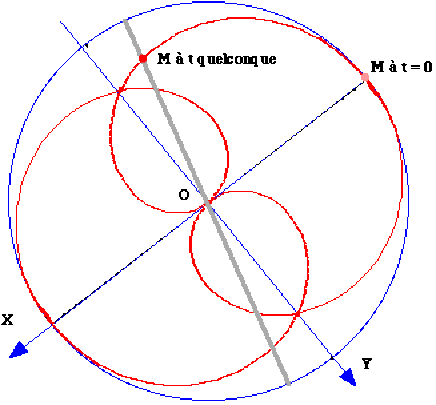
En éliminant le temps entre les variables, on obtient l'équation de la trajectoire
\(\displaystyle{x_1(\theta)=A.\cos\frac{\omega_0}{\Omega}(\theta-\theta_0)}\)
La trajectoire est un limaçon de Pascal.
La courbe ci-dessous correspond à la valeur\( \displaystyle{\Omega=2\omega_0}\)