Oscillations

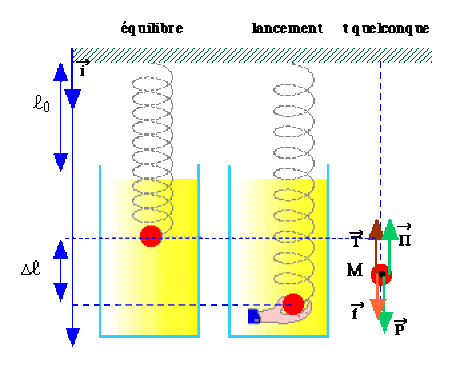
3) -- On plonge la bille dans un liquide de manière que la poussée d'Archimède équilibre le poids. Soit \(\overrightarrow\pi\) cette poussée. On est en présence de quatre forces :

- le poids \(\overrightarrow P=mg\overrightarrow i\).

- la force de tension \(\displaystyle{\overrightarrow T=-k(x-l_0)\overrightarrow i}\)

- la poussée d'Archimède\( \displaystyle{\overrightarrow\pi=-\overrightarrow P}\)

- la force de freinage\( \displaystyle{\overrightarrow f=-k'\overrightarrow v}\).

Puisque \(\overrightarrow\pi\) équilibre le poids \(\displaystyle{\overrightarrow P=mg\overrightarrow i}\) , le ressort reprend sa valeur \(\displaystyle{l_0}\) et lorsqu'on l'écarte de \(\Delta l\) , il se déplace, en étant freiné, autour de la position \(\displaystyle{l_0}\) . La nature du mouvement dépend des valeurs des paramètres.

Le principe fondamental nous donne :

\(\displaystyle{\overrightarrow P+\overrightarrow T+\overrightarrow\pi+\overrightarrow f=m\overrightarrow a}\)

soit selon le vecteur de base \(\overrightarrow i\)

\(\displaystyle{mg\overrightarrow i+\overrightarrow\pi-k(x-l_0)\overrightarrow i-k'x'\overrightarrow i=mx"\overrightarrow i}\)

avec

\(\displaystyle{mg\overrightarrow i+\overrightarrow\pi=\overrightarrow0}\)

on passe alors en coordonnées réduites avec \(\displaystyle{\omega_0^2=\frac{k}{m}}\) et \(\displaystyle{2\lambda=\frac{k'}{m}}\) , l'équation du mouvement prend alors la forme générale suivante :

\(\displaystyle{\ddot x+2\lambda\dot x+\omega_0^2x=\omega_0^2l_0}\)

• La solution particulière de l'équation différentielle totale est \(\displaystyle{x_p=l_0}\) .

• La solution générale de l'équation sans second membre (équation différentielle homogène du second ordre à coefficients constants) se détermine en cherchant des solutions de la forme \(\textrm e^{-rt}\) . On cherche les solutions de l'équation caractéristique

  \(\displaystyle{r^2+2\lambda r+\omega_0^2=0}\)

  Si \(r_1\) et\( r_2\) sont les solutions de l'équation caractéristique et \(A_1 \textrm{ et }A_2\) constantes d'intégration déterminées par les conditions initiales, la solution générale est de la forme

  \(\displaystyle{x(t)=A_1\textrm e^{r_1t}+A_2\textrm e^{r_2t}}\)

• La solution générale de l'équation avec second membre est

  \(\displaystyle{x(t)=x_p+x(t)=A_1\textrm e^{r_1t}+A_2\textrm e^{r_2t}+l_0}\)

  et ce sont les conditions initiales qui permettent de calculer \(A_1 \textrm{ et }A_2\)

  a) Quand les racines de l'équation caractéristique sont réelles, elles sont négatives et le mouvement est rapidement amorti : on dit que le régime est apériodique :

  \(\displaystyle{x(t)=A_1\textrm e^{-\rho_1^t}}+A_2\textrm e^{-\rho_2^t}\)

  avec \(\displaystyle{\rho_1=\vert r_1\vert\textrm{ et }\rho_2=\vert r_2\vert}\)

  Avec les paramètres de l'énoncé, ce type de solution a lieu pour \(\displaystyle{\lambda^2-\omega_0^2>0}\) soit pour \(\displaystyle{\frac{k^{'2}}{4k}> m}\)

  A.N.\( \displaystyle{\frac{k^{'2}}{4k}=0,0225}\) qui est en effet supérieur à la valeur donnée de \(m (= 0,020 \textrm{ K})\).

  b) Quand les racines de l'équation caractéristique sont imaginaires, elles sont conjuguées et on a un régime oscillant amorti de la forme

  \(\displaystyle{x(t)=A\textrm e^{-\lambda t}\cos(\omega t+\phi)}\)

  où \(\omega\) est tel que \(\displaystyle{\omega^2=\omega_0^2-\lambda^2}\) et la solution complète est :

  \(\displaystyle{X(t)=x_p+x(t)=-l_0+A\textrm e^{-\lambda t}\cos(\omega t+\phi)}\)

  Rappel : ce n'est que sur la forme complète qu'on détermine les constantes d'intégration.

  c) La racine double négative \(r_1 = - \lambda\) correspond à "l'amortissement critique". C'est la limite entre l'amortissement et les oscillations. La solution est alors égale à

  \(\displaystyle{x(t)=(A_1+A_2t)\textrm e^{-\lambda t}}\)

  C'est pour \(m = 22,5 \textrm{ g}\) que l'on est ici dans le cas critique. Pour cette valeur de \(m\), le retour à l'équilibre est le plus rapide. \(\lambda\) est alors égal à \(\omega_c\) tel que\( \displaystyle{\omega_c^2=\frac{k}{m_c}}\).

  La solution complète du régime critique est

  \(\displaystyle{x(t)=-l_0+(A_1+A_2t)\textrm e^{-\lambda t}}\)

  avec pour\( t = 0\) :\( \displaystyle{X(t)=l_0+\Delta l}\) et \(X'(t) = 0\), ce qui donne\( \displaystyle{A_1=\Delta l\textrm{ et }A_2=\lambda\Delta l}\) .

  D'où

  \(\displaystyle{X(t)=-l_0+\Delta l(1+\lambda t)\textrm e^{-\lambda t}=-l_0+\Delta l(1+\omega_ct)\textrm e^{-\omega_ct}}\)

  A.N. \(\displaystyle{\lambda=\frac{k'}{2m}=13,33}\)

  et

  \(\displaystyle{X(t)+l_0=+49.10^{-3}(1+13,3t)\textrm e^{-13,3t}}\)

  Au bout du temps \(t = 0,5 \textrm{ s}\),

  \(\displaystyle{\frac{(X(1/2)+l_0)}{\Delta l}=7,66\textrm e^{-6,66}}\)