Intégrale de Laplace [Synthèse]

Intégrale de Laplace

Partie

Question

Intégrale de Laplace (***)

Soit un référentiel galiléen, muni du repère sphérique $(O,\overrightarrow u_r,\overrightarrow u_\theta,\overrightarrow u_\Phi)$ .Une particule $P$ , de masse $m$ , est placée dans le champ de forces central:

$\displaystyle{\overrightarrow F(M)=\frac{-k}{r^2}\overrightarrow u_r}$

où $k$ est une constante positive, différente de $0$ .

A partir du théorème du moment cinétique, déduire que le moment cinétique $\overrightarrow\sigma$ est constant. Montrer que la trajectoire de la particule est plane.
Dans les questions suivantes, on utilise un repère cylindrique $(O,\overrightarrow u_\rho,\overrightarrow u_\Phi,\overrightarrow k)$ . Le vecteur unitaire $\overrightarrow k$ sera pris orthogonal au plan de la trajectoire. On pose alors $\overrightarrow\sigma=\sigma_0\overrightarrow k$ et la force appliquée à la particule s'écrit maintenant:
$\displaystyle{\overrightarrow F(M)=\frac{-k}{\rho^2}\overrightarrow u_\rho}$
Exprimer $\sigma_0$ en fonction de $\displaystyle{m,\rho\textrm{ et }\Phi}$
Quelle relation existe entre $\displaystyle{\dot\Phi\frac{\textrm d\overrightarrow u_\Phi}{\textrm dt}\textrm{ et }\overrightarrow u_\rho}$
A partir du théorème de la quantité de mouvement et l'équation vectorielle correspondante pour la particule $P$ , déduire de ce qui précède que le vecteur vitesse peut se mettre sous la forme
$\displaystyle{\overrightarrow V=\frac{k}{\sigma_0}(\overrightarrow u_\Phi+\overrightarrow H)}$
où $\overrightarrow H$ est un vecteur constant. Montrer que la composante selon $\overrightarrow u_\Phi$ du vecteur vitesse est égale à
$\displaystyle{\frac{\sigma_0}{m\rho}}$
La trajectoire est elliptique de foyer $O$ et d'équation $\displaystyle{\frac{1}{\rho}=\frac{1}{p}+\frac{\textrm e}{p}\cos\Phi}$ où $\textrm e$ est l'excentricité de l'ellipse et $p$ son paramètre.
On note $S$ la position du périgée (point où la distance $OP$ est minimum). En considérant la vitesse de la particule en $S$ , déterminer la direction de $\overrightarrow H$ . En utilisant notamment ce dernier résultat, déterminer complètement le vecteur $\overrightarrow H$ . Représenter en un point quelconque de la trajectoire elliptique et au point $S$ , les vecteurs $\displaystyle{\overrightarrow F,\overrightarrow V\textrm{ et }\overrightarrow H}$ .
On donne $\displaystyle{p=\frac{\sigma_0^2}{mk}}$ .

Aide simple

Solution détaillée

Dans un référentiel galiléen, la dérivée par rapport au temps du moment cinétique d'un point matériel par rapport à un point A fixe dans ce référentiel, est égale au moment résultant par rapport au même point A des forces appliquées au point matériel.
$\displaystyle{\frac{\textrm d\overrightarrow\sigma_A}{\textrm dt}=\overrightarrow N(A)=\overrightarrow{OM}\wedge\overrightarrow F(M)}$
Or, $\displaystyle{\overrightarrow F(M)=\frac{-k}{r^2}\overrightarrow u_r\textrm{ et }\overrightarrow{OM}=r\overrightarrow u_r}$
Par suite du produit vectoriel, $\displaystyle{\frac{\textrm d\overrightarrow\sigma_A}{\textrm dt}=\overrightarrow0}$
donc $\overrightarrow\sigma$ est un vecteur constant perpendiculaire au plan défini par $\overrightarrow{OM}$ et $\overrightarrow v$ ,donc le plan de la trajectoire est constant : la trajectoire est plane.
Par définition,
$\overrightarrow\sigma=\overrightarrow{OM}\wedge m\overrightarrow v=\rho\overrightarrow u_\rho\wedge m\overrightarrow v\textrm { or } : \overrightarrow v=\dot\rho\overrightarrow u_\rho+\rho\dot\Phi\overrightarrow u_\Phi$
d'où $\displaystyle{\overrightarrow\sigma=m\rho^2\dot\Phi\overrightarrow u_\rho\wedge\overrightarrow u_\Phi=m\rho^2\dot\Phi\overrightarrow k=\sigma_0\overrightarrow k\textrm{ et }\sigma_0=m\rho^2\dot\Phi}$
La relation existant entre $\displaystyle\frac{\textrm d\overrightarrow u_\Phi}{\textrm dt},\dot\Phi\textrm{ et }\overrightarrow u_\rho$ , s'obtient en effectuant une dérivation composée
$\displaystyle{\frac{\textrm d\overrightarrow u_\Phi}{\textrm dt}=\frac{\textrm d\overrightarrow u_\Phi}{\textrm d\Phi}\frac{\textrm d\Phi}{\textrm dt}=\dot\Phi\frac{\textrm d\overrightarrow u_\Phi}{\textrm d\Phi}=-\dot\Phi\overrightarrow u_\rho}$
Dans un référentiel galiléen, la résultante des forces appliquées à un point matériel est égale à la dérivée par rapport au temps du vecteur quantité de mouvement.
$\displaystyle{\overrightarrow F=\frac{\textrm d\overrightarrow mv}{\textrm dt}=\frac{\textrm d\overrightarrow p}{\textrm dt}}$
$\frac{ \textrm d \overrightarrow mv }{ \textrm dt } = m \frac{ \textrm d }{ \textrm dt }(\dot\rho\overrightarrow u_\rho + \dot\Phi\overrightarrow u_\Phi)=-\frac{k}{\rho^2}\overrightarrow u_\rho$
d'où $\displaystyle{\frac{\textrm d\overrightarrow v}{\textrm dt}=-\frac{k}{m\rho^2}\overrightarrow u_\rho}$ . Or, on a vu que
$\displaystyle{\dot\Phi=\frac{\sigma_0}{m\rho^2}\textrm{ et que }\frac{\textrm d\overrightarrow u_\Phi}{\textrm dt}=-\dot\Phi\overrightarrow u_\rho}$
ce qui donne $\frac{\textrm d\overrightarrow v}{\overrightarrow{\textrm dt}}= \frac{k}{\sigma_0} \frac{\textrm d\overrightarrow u_\Phi}{\textrm dt} \textrm{ avec } \frac{k}{\sigma_0}= \textrm{cste}$ .
En intégrant $\displaystyle{\overrightarrow v=\frac{k}{\sigma_0}(\overrightarrow u_\Phi+\overrightarrow H)}$
où $\overrightarrow H$ est un vecteur constant d'intégration.
La composante selon $\overrightarrow u_\Phi$ du vecteur vitesse est égale par définition à :
$\displaystyle{\overrightarrow v\cdot\overrightarrow u_\Phi=\rho\dot\Phi=\frac{\sigma_0}{m\rho}}$
Cette composante est aussi égale à
$\displaystyle{\overrightarrow v\cdot\overrightarrow u_\Phi=\frac{k}{\sigma_0}+\frac{k}{\sigma_0}(\overrightarrow u_\Phi\cdot\overrightarrow H)}$
de la même manière
$\displaystyle{\overrightarrow v\cdot\overrightarrow u_\rho=\frac{k}{\sigma_0}(\overrightarrow u_\rho\cdot\overrightarrow H)=\dot\rho}$
étant constant, on choisit pour le déterminer un point où on connait $\overrightarrow v$ : en $S$ , $\overrightarrow v$ est selon $\overrightarrow u_\Phi$ et est égal à $\displaystyle{\overrightarrow v(S)=\rho_{\textrm{min}}\dot\Phi\overrightarrow u_\Phi}$ ;
par suite, $\displaystyle{\overrightarrow v=\frac{k}{\sigma_0}(\overrightarrow u_\Phi+\overrightarrow H)}$
est aussi selon $\overrightarrow u_\Phi$ et sa norme est constante.
On a vu que $\displaystyle{\overrightarrow v\cdot\overrightarrow u_\Phi=v_\Phi=\frac{\sigma_0}{m\rho}=\frac{\sigma_0}{m}(\frac{1}{p}+\frac{\textrm e}{p}\cos\Phi)}$

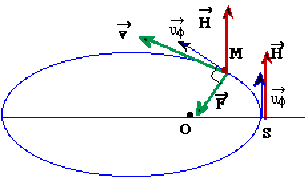
Au point $S$ : $\displaystyle{v_\Phi=\frac{\sigma_0}{mp}(1+\textrm e)=\frac{k}{\sigma_0}(1+\Vert\overrightarrow H\Vert)}$

On déduit que $\displaystyle{\Vert\overrightarrow H\Vert=\textrm e}$

:l'excentricité de l'ellipse car $\displaystyle{p=\frac{\sigma_0^2}{mk}}$

La grandeur est une intégrale première du mouvement, c'est l'intégrale de Laplace :

$\displaystyle{\overrightarrow H=\textrm e\overrightarrow u_{\Phi(S)}}$