Oscillations
Partie
Question
Oscillations sinusoïdales d'une masse glissant sur une tige en rotation libre (**)
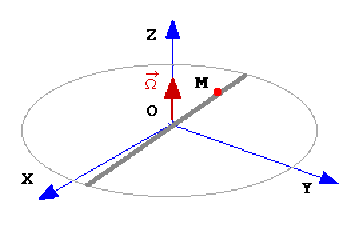
Un point matériel \(M\) de masse m est assujetti à se déplacer sans frottements sur une tige horizontale, sur laquelle il effectue des oscillations sinusoïdales dont la loi de variation en fonction du temps est :
\(\displaystyle{\rho=\rho_0(2+\cos\omega_0t)\textrm{ avec }\rho>0}\)
La tige \(OM\) tourne librement autour de l'axe vertical \(OZ\).
Son vecteur rotation instantanée est noté \(\overrightarrow\Omega\) et on notera \(\overrightarrow\Omega_0\) la valeur initiale donnée à la rotation de la tige.
Etudier le mouvement du point M par rapport au référentiel (\(O, XYZ\)).
Exprimer la force nécessaire pour produire ces oscillations.
Aide simple
Il s'agit d'un problème de dynamique, dans lequel il faut traduire le couplage entre le mouvement de la masse m par rapport à la tige, et le mouvement de rotation de la tige.
Avant de chercher la force qui produit les oscillations, analyser toutes les forces agissant sur la masse \(m\).
Les oscillations de la masse m sont sinusoïdales forcées. Ce qui suppose qu'un oscillateur exerce sur cette masse une force de grandeur a priori inconnue, dont seule la direction est connue (selon \(OM\)).
Choisir une méthode de traitement, et les théorèmes utiles pour résoudre
Solution détaillée
Le mouvement "relatif" est celui par rapport au référentiel [\(R\)] lié à la tige. On l'exprime dans le repère cylindrique \((O,\overrightarrow u_\rho,\overrightarrow u_\theta,\overrightarrow k )\) car \(\rho\) est \(> 0\).
Le mouvement "absolu" est celui par rapport au référentiel [\(Ra\)] lié au laboratoire. On l'exprime dans la base cartésienne \((O,\overrightarrow i,\overrightarrow j,\overrightarrow k)\) .
La tige tourne autour de l'axe vertical \(OZ\), à vitesse angulaire variable. Son vecteur rotation instantanée est noté \(\displaystyle{\overrightarrow\Omega=\theta'\overrightarrow k}\) .
Le mouvement de la masse selon s'écrit :
\(\rho = \rho_0 ( 2 + \cos \omega_0t )\)
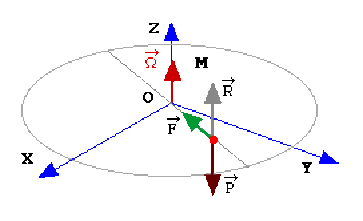
Le principe fondamental s'écrit sous sa forme vectorielle avec le poids \(\overrightarrow P\) , la réaction \(\overrightarrow R\) qui s'exerce sur la masse, et la force\( \overrightarrow F\) qui produit le mouvement sinusoïdal sur la tige.
\(\displaystyle{m\overrightarrow\gamma_a=\overrightarrow P+\overrightarrow R+\overrightarrow F\quad(1)}\)
\(\displaystyle{\overrightarrow R=R_1\overrightarrow u_\rho+R_2\overrightarrow u_\theta+R_3\overrightarrow k}\)
où \(R_1, R_2 \textrm{ et }R_3\) sont à déterminer.
Or, la force \(\overrightarrow F\) est centrale : sa direction est colinéaire à \(\overrightarrow u_\rho\) . Par conséquent, on sait que le moment cinétique est une constante du mouvement. La décomposition de (1) dans la base "relative" \((O,\overrightarrow u_\rho,\overrightarrow u_\theta,\overrightarrow k)\) conduit aux équations
\(\displaystyle{R_3-mg=m\frac{\textrm d^2z}{\textrm dt^2}=0\quad(2)}\)
car le mouvement est plan.
\(\displaystyle{R_1+F=m(\frac{\textrm d^2\rho}{\textrm dt^2}-\rho\Omega^2)\quad(3)}\)
\(\displaystyle{R_2=m.(2\frac{\textrm d\rho}{\textrm dt}\Omega+\rho\frac{\textrm d\Omega}{\textrm dt})\quad(4)}\)
La condition d'absence de frottement entre la tige et le point M impose que le travail de la réaction au cours du déplacement relatif (M sur tige) soit identiquement nul :
\(\displaystyle{\overrightarrow R\cdot\overrightarrow{\textrm dM}=0\iff R_1=0}\)
d'où la nouvelle expression de (3) qui permet d'exprimer la force :
\(\displaystyle{F=m.(\frac{\textrm d^2\rho}{\textrm dt^2}-\rho\Omega^2)\quad(3')}\)
La tige est en rotation libre, donc il ne s'exerce sur elle aucun couple et la composante de la réaction selon est nulle :
\(R_2 = 0\). Alors, la nouvelle forme de la relation (4) exprime la loi des aires :
\(\displaystyle{\frac{\textrm d}{\textrm dt}(\rho^2\Omega)=0\iff\Omega(t)=\frac{C}{\rho^2}\quad(4')}\)
Le mouvement de la masse selon permet d'exprimer \(\displaystyle{\rho_0\cos\omega_0t=\rho-2\rho_0}\)
La relation (3') permet ainsi d'obtenir l'expression de la force :
\(\displaystyle{F(t)=m[-\omega_0^2\rho_0\cos\omega_0t-\frac{C^2}{\rho^3}]}\)
En utilisant\( \displaystyle{\overrightarrow F=-\overrightarrow{\textrm{grad}}U}\) , et sachant que la force \(\overrightarrow F\) exercée sur m est de la forme \(F_{\overrightarrow u_\rho}\) , on détermine le potentiel \(U\) (à une constante près) :
\(\displaystyle{U=m[\frac{\omega_0^2\rho^2}{2}-2\omega_0\rho_0\rho-\frac{C^2}{2\rho^2}]}\)
L'énergie cinétique de m s'exprime :
\(\displaystyle{T=(\frac{m}{2})(V_r^2+V_e^2)=(\frac{m}{2})[(\frac{\textrm d\rho}{\textrm dt})^2+\rho^2\Omega^2]}\)
En utilisant la relation des aires :\( \displaystyle{\Omega(t)=\frac{C}{\rho^2}(t)}\)
, on obtient :
\(\displaystyle{T=(\frac{m}{2}).(\frac{(\frac{\textrm d\rho}{\textrm dt})^2+C^2}{2\rho^2})}\)
La variation \(\textrm dT\) d'énergie cinétique est égale au travail élémentaire de la force \(\overrightarrow F\) sur un déplacement , soit :
\(\displaystyle{\textrm d\overrightarrow T=\overrightarrow F.\textrm d\overrightarrow{M}=-\overrightarrow{\textrm{grad}}U.\textrm d\overrightarrow{M}}\)
Par définition : \(\displaystyle{\overrightarrow{\textrm{grad}}U.\textrm d\overrightarrow M=\textrm dU}\)
. La variation d'énergie cinétique est donc : \(\textrm dT = - \textrm dU \textrm{ d'où }\textrm dT + \textrm dU = \textrm d (T+U) = \textrm dE = 0\)
L'énergie totale \(E=T + U\) est donc constante.
Ce système présente l'énergie et le moment cinétique comme une constante du mouvement. Les trajectoires ne constituent pas des formes mathématiques simples.