Mouvement d'une masse fixée à un ressort tournant à vitesse angulaire constante
Partie
Question
Mouvement d'une masse fixée à un ressort tournant à vitesse angulaire constante (*)
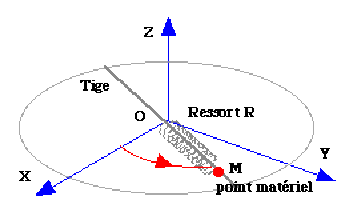
Soit le référentiel du laboratoire supposé galiléen. Il est muni du repère cartésien et le vecteur unitaire \(\overrightarrow k\) est dirigé dans le sens de la verticale ascendante. Un point matériel \(M\) de masse \(m\) est assujetti à se déplacer sans frottement sur une tige horizontale \(\Delta\) . Il est attaché à l'une des extrémités d'un ressort \(R\) de dureté \(K\) qui coulisse lui aussi sans frottement le long de la tige \(\Delta\) , et dont l'autre extrémité est fixée au point \(O\). Soit\( (O,\overrightarrow u_\rho,\overrightarrow u_\theta,\overrightarrow k)\) le cylindrique tel que \(\overrightarrow u_\rho\) soit dirigé de \(O\) vers \(M\). La tige \(\Delta\) est assujettie à tourner autour de l'axe vertical \(O_z\) avec une vitesse angulaire constante.Son vecteur rotation est noté \(\overrightarrow\Omega\) . L'allongement du ressort est égal à \((\rho-l_0)\)
où est la longueur à vide du ressort et \(\rho\) sa longueur à un instant quelconque.
On suppose que la masse de la tige est négligeable par rapport à la masse \(m\) du point \(M\). On pose :
\(\displaystyle{\omega_0^2=\frac{K}{m}.At=0,OM_0=\rho_0,\theta_0=0,\rho'=0}\)
Le but du problème est d'étudier le mouvement du point \(M\) par rapport à la tige.
Comment sont dirigées ,\(\displaystyle{\overrightarrow\gamma_a,\overrightarrow\gamma_e,\overrightarrow\gamma_c ?}\) , Exprimer les vecteurs accélérations intervenant dans le système en rotation dans le repère cylindrique.
Faire l'inventaire des forces agissant sur la masse \(m\); on posera a priori la réaction de la tige sur la masse
\(\displaystyle{\overrightarrow R=X\overrightarrow u_\rho+Y\overrightarrow u_\theta+Z\overrightarrow k}\)
Exprimez ces forces dans la base cylindrique.
Donner alors la valeur des composantes de la réaction de la tige.
Comment doit-être le moment cinétique? Pourquoi? Donner son expression dans la base cylindrique.
Aide simple
Il faut traduire le couplage entre le mouvement de la masse m par rapport à la tige, et le mouvement de rotation de la tige.
Le système est le point \(M\). L'extérieur du système est constitué de la tige et du champ de pesanteur terrestre. L'action de l'extérieur se traduit par une réaction a priori inconnue.
Solution détaillée
1) On définit le référentiel [\(R\)] "relatif" à partir du repère cylindrique : \((O,\overrightarrow u_\rho,\overrightarrow u_\theta,\overrightarrow k)\) lié à la tige. Le référentiel [\(R_a\)] "absolu" est celui du laboratoire : \((O,\overrightarrow i,\overrightarrow j,\overrightarrow k)\) .
Le point matériel\( M\), assujetti à se déplacer sans frottement sur la tige qui l'entraine à vitesse de rotation constante autour de l'axe vertical \(OZ\), est soumis, par rapport au galiléen lié au laboratoire, à l'accélération
\(\displaystyle{\overrightarrow\gamma_a=\overrightarrow\gamma_r+\overrightarrow\gamma_e+\overrightarrow\gamma_c}\)
\(\displaystyle{\overrightarrow\gamma_r=\rho"\overrightarrow u_\rho}\)
\(\displaystyle{\overrightarrow\gamma_e=\overrightarrow\Omega'\wedge\overrightarrow{OM}+\overrightarrow\Omega\wedge[\overrightarrow\Omega\wedge\overrightarrow{OM}]=\rho\Omega'\overrightarrow u_\theta-\rho\Omega^2.\overrightarrow u_\rho}\)
\(\displaystyle{\overrightarrow\gamma_c=2\overrightarrow\Omega\wedge\overrightarrow V_r=2\rho'\Omega\overrightarrow u_\theta}\)
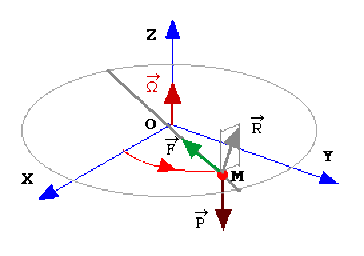
2) Le point matériel \(M\) est soumis à trois forces : le poids \(\overrightarrow P\) , la réaction \(\overrightarrow R\) du support, la force de tension \(\overrightarrow T\) du ressort qui est égale à \(\displaystyle{-K(\rho-l_0)\overrightarrow u_\rho}\).
Le principe fondamental s'écrit sous forme vectorielle :
\(\displaystyle{\overrightarrow P+\overrightarrow R+\overrightarrow T=m\overrightarrow\gamma_a\quad(1)}\)
avec \(\displaystyle{\overrightarrow R=X\overrightarrow u_\rho+Y\overrightarrow u_\theta+Z\overrightarrow k}\) où \(X,Y \textrm{ et }Z\) sont à déterminer.
Le mouvement étant plan, la composante de la réaction selon la verticale équilibre le poids.
La décomposition de (1) dans la base "relative" conduit aux trois équations : par suite :
\(\displaystyle{Z-mg=m.z"=0\quad(2)}\)
\(\displaystyle{-K(\rho-l_0)+X=m(\rho"-\rho\Omega^2)\quad(3)}\)
\(\displaystyle{Y=m.2\rho'\Omega\quad(4)}\)
3) La relation (4) détermine la composante \(Y\) de \(\overrightarrow R\) selon \(\overrightarrow u_\theta\) qui s'oppose à l'action du point coïncidant avec \(M\) de la tige lors du mouvement imposé à \(\Omega\) constant. Il faut maintenant traduire la condition d'absence de frottement entre la tige et le point \(M,\) à savoir que le travail de la réaction au cours du déplacement relatif (\(M\) sur tige) est identiquement nul :
\(\displaystyle{\overrightarrow R\cdot\overrightarrow{\textrm dM}=0\iff X=0}\)
La réaction s'exprime donc dans la base cylindrique par :
\(\displaystyle{\overrightarrow R=0\overrightarrow u_\rho+m.2\rho'\Omega\overrightarrow u_\theta+mg\overrightarrow k}\)
Dans le plan orthogonal à la tige, la réaction traduit les effets du plan et de la tige en mouvement.
4) Le moment cinétique par rapport au point \(O\) s'écrit par définition :
\(\displaystyle{\overrightarrow\sigma=\sigma\overrightarrow u_\rho\wedge m\overrightarrow v}\)
où est la somme de\( \displaystyle{\rho'\overrightarrow u_\rho+\rho\Omega.\overrightarrow u_\theta}\) ; on trouve alors
\(\displaystyle{\overrightarrow\sigma=\rho\Omega^2\overrightarrow k}\)
La direction du moment cinétique est fixe, ce qu'on pouvait prévoir car la trajectoire est plane. La vitesse de rotation est constante mais par contre, le rayon vecteur ne l'est pas : le moment cinétique n'est pas constant.