Systèmes centrés-Equation de conjugaison-Lentilles minces
Partie
Question
Etablir dans l'approximation des sommets confondus et dans l'air, la distance focale image du système composé de deux lentilles minces \(L, L'\), accolées d'indice de réfraction et rayons des faces (1) et (2) respectifs \(N, N', R_1, R_{2}, R'_{1}, R'_{2}\).
A.N. : \(R'_{1} = R_2 ; N = N' = 1,5\)
\(R_{1} = -R_{2} = -R'_{1} = -2.R'_{2} = \mathrm{0,1} \textrm {m}\)
Considérer les différents dioptres sphériques constitutifs.
Aide simple
La distance focale image \(f '\) d'une lentille mince est la mesure algébrique du segment \(\overline{SF'}\) qui sépare le sommet \(S\) de l'image \(F'\) d'un point de l'axe infiniment éloigné de \(S\).
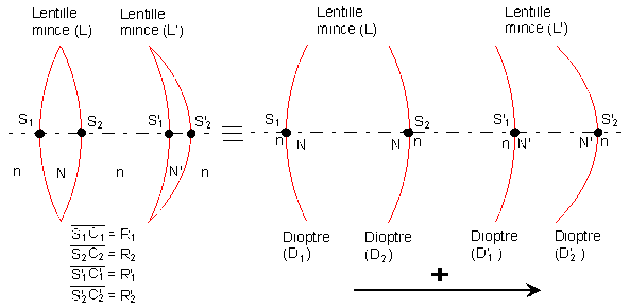
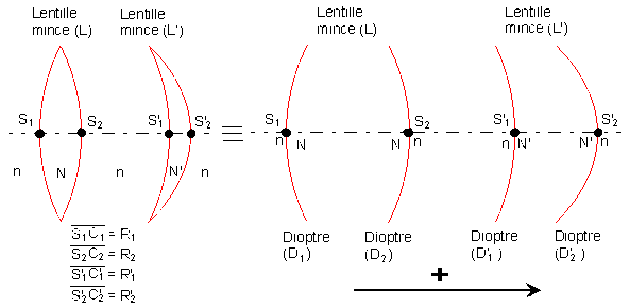
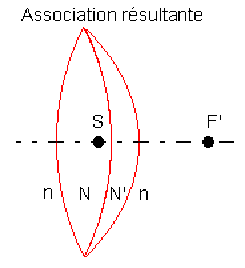
Dans l'approximation des sommets confondus, l'association de lentilles minces se comporte comme une lentille unique mais aussi comme une association de quatre dioptres sphériques \(D_{1}, D_{2}, D'_{1}, D'_{2}\) qui auraient un seul et même sommet : \(S\).
Aide détaillée
Le système est une association de quatre dioptres sphériques \((D_{1}),(D_{2}),(D'_{1}),(D'_{2})\) centrés par un même axe. L'image de tout point de l'axe fournie par l'un quelconque de ces dioptres est vue comme un objet (réel ou virtuel) par le dioptre suivant.
L'image \(F'\) du point \(A\) à l'infini est le résultat de quatre transformations objet - image, par chaque dioptre traversé, qui obéissent toutes à l'équation de conjugaison du dioptre sphérique de rayon \(R = \overline{SC}\) qui sépare un milieu d'indice \(n_{1},\) d'un milieu d'indice \(n_{2}.\)
\(\frac{n_{2}}{\overline{SA_{2}}} - \frac{n_{1}}{\overline{SA_{1}}} = \frac{n_{2} - n_{1}}{\overline{SC}}\)
En plus :
La lumière issue du point \(A\) rencontre successivement les quatre dioptres
\((D_{1}),(D_{2}),(D'_{1}),(D'_{2})\). Soient \(A_{1},A'_{1},A'\) et \(A'_{2}\) les images fournies par chacun de ces dioptres du point objet perçu (\(A\) pour \(D_{1},\) \(A_{1}\) pour \(D_{2},\) \(A'_{1}\) pour \(D'_{1}\) et \(A'\) pour \(D'_{2}\)).
Rappel de cours
Le dioptre sphérique n'est rigoureusement stigmatique que pour les points de sa surface et son centre
Il y a stigmatisme approché pour tout point de l'espace qui n'envoie sur le dioptre sphérique qu'un pinceau lumineux dont le rayon moyen lui est normal, c'est à dire peu incliné par rapport à l'axe du dioptre ou encore formé de rayons paraxiaux.
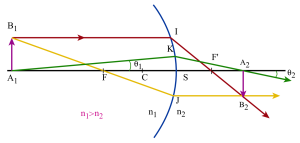
Tout rayon incident parallèle à l'axe optique se réfracte en passant par le foyer image F'.
Un rayon incident passant par le foyer objet du dioptre se réfractera en un rayon parallèle à l'axe optique du dioptre.
Pour construire l'image d'un objet plan :
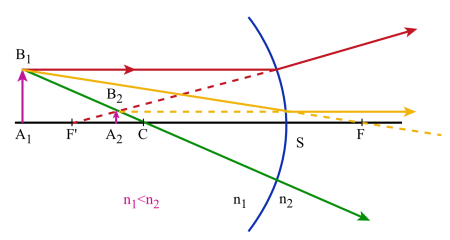
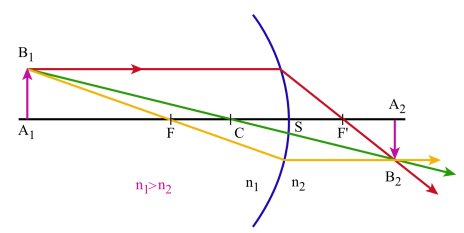
on utilise 3 rayons particuliers :
un rayon passant par le centre du dioptre et qui n'est pas dévié à la traversée de celui-ci
un rayon issu de \(B_1\) et passant par le foyer objet \(F\) : il est réfracté suivant une parallèle à l'axe principal
un rayon issu de \(B_1\) et parallèle à l'axe principal : il est réfracté suivant un rayon qui passe par le foyer image \(F'\).
Formules de conjugaison :
Origine au sommet
\(\frac{n_1}{\overline{SA_1}}.\frac{n_2}{\overline{SA_2}}=\frac{n_1-n_2}{\overline{SC}}\)
\(\gamma=\frac{n_1}{n_2}\frac{\overline{SA_2}}{\overline{SA_1}}\)
Origine au centre
\(\frac{n_{1}}{\overline{CA_{2}}}.\frac{n_{2}}{\overline{CA_{1}}}=\frac{n_{1}-n_{2}}{\overline{CS}}\)
\(\gamma=\frac{\overline{A_2B_2}}{\overline{A_1B_1}}=\frac{\overline{CA_2}}{\overline{CA_1}}\)
Origine aux foyers
\(\overline{FA_1}\overline{F'A_2}=\overline{SF}\overline{SF'}=ff'\)
\(\gamma=-\frac f{\overline{FA_1}}=\frac{\overline{F'A_1}}{f'}\)
Relation de Lagrange-Helmholtz :
Solution détaillée
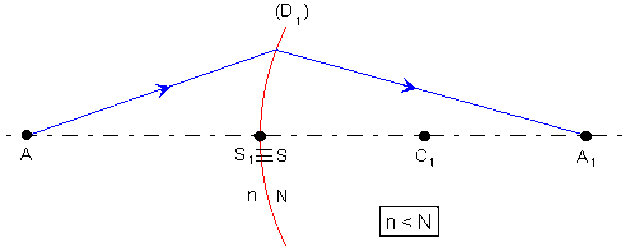
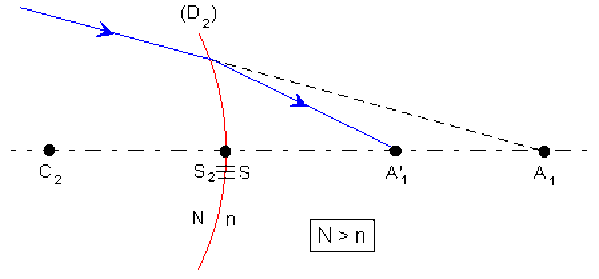
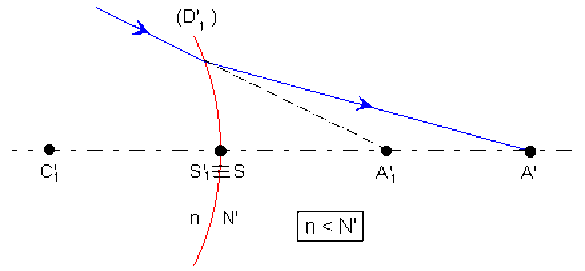
La lumière issue du point \(A\) rencontre successivement les quatre dioptres
\((D_{1}), (D_{2}), (D'_{1}), (D'_{2})\). Soient \(A_{1}, A'_{1}, A'\) et \(A'_{2}\) les images fournies par chacun de ces dioptres du point objet perçu (\(A\) pour \(D_1\), \(A_1\) pour \(D_2\), \(A'_{1}\) pour \(D'_{1}\) et \(A'\) pour \(D'_{2}\)).
L'équation de conjugaison du dioptre sphérique, origine au sommet \(S\), s'écrit pour chacun de ces quatre couples objet - image.
\(A\substack{{D_1}\\{\substack{{\longrightarrow}\\{n\rightarrow N}}}}A_1\quad A'_{1}\substack{{D'_1}\\{\substack{{\longrightarrow}\\{n\rightarrow N'}}}}A'\)
\(\frac N{\overline{SA_1}}-\frac n{\overline{SA}}=\frac{N-n}{\overline{SC_1}}=\frac{N-n}{R_1}\frac{N'}{\overline{SA'}}-\frac n{\overline{SA'_{1}}}=\frac{N'-n}{\overline{SC'_1}}=\frac{N-n}{R'_1}\)
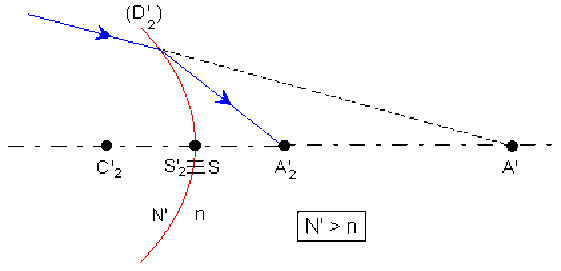
\(A_{1}\substack{{D_{2}}\\{\substack{{\longrightarrow}\\{N\rightarrow n}}}}A'_1\quad A'\substack{{D'_{2}}\\{\substack{{\longrightarrow}\\{N'\rightarrow n}}}}A'_{2}\)
\(\frac n{\overline{SA'_{1}}}-\frac N{\overline{SA_1}}=\frac{n-N}{\overline{SC_2}}=-\left(\frac{N-n}{R_2}\right)\frac n{\overline{SA'_{2}}}-\frac{N'}{\overline{SA'}}=\frac{n-N'}{\overline{SC'_2}}=-\left(\frac{N'-n}{R'_2}\right)\)
par addition : pour \(L\) pour \(L'\)
\(\frac n{\overline{SA'_{1}}}-\frac n{\overline{SA}}=(N-n)\cdot\left(\frac1{R_{1}}-\frac1{R_{2}}\right)\frac n{\overline{SA'_{2}}}-\frac n{\overline{SA'_{1}}}=(N'-n)\cdot\left(\frac1{R'_{1}}-\frac1{R'_{2}}\right)\)
D'où l'image \(A'_{2}\) de \(A\) par le système :
\(\frac n{\overline{SA'_{2}}}-\frac n{\overline{SA}}=(N-n)\cdot\left(\frac1{R_{1}}-\frac1{R_{2}}\right)+(N'-n)\cdot\left(\frac1{R'_{1}}-\frac1{R'_{2}}\right)\)
et la distance focale \(\overline{SF'}=\overline{SA'_{2}}\) lorsque \(\overline{SA}\rightarrow\infty\) et si \(N = N' ; R'_{1} = +R_{2}\).
\(\frac n{\overline{SF'}}=(N-n)\cdot\left(\frac1{R_{1}}-\frac1{R'_{2}}\right)\)
A.N. : \(\frac1{f'}=(+0,5)\cdot\left(\frac1{0,1\textrm m}-\frac1{-0,05\textrm m}\right)\)
\(\frac1{f'}=(+0,5)\cdot(10+20)=15 \textrm m^{-1}\)
\(f'=0,067\textrm m\)
\(A\substack{{D_1}\\{\substack{{\longrightarrow}\\{n\rightarrow N}}}}A_1\)
\(A_{1}\substack{{D_2}\\{\substack{{\longrightarrow}\\{N\rightarrow n}}}}A'_1\)
\(A'_{1}\substack{{D'_1}\\{\substack{{\longrightarrow}\\{n\rightarrow N'}}}}A'\)
\(A'\substack{{D'_2}\\{\substack{{\longrightarrow}\\{N'\rightarrow n}}}}A'_{2}\)