Stigmatisme
Partie
Question
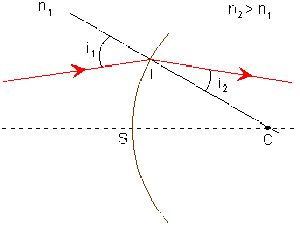
Vérifier par construction approchée, que tout point de la surface d'un dioptre est sa propre image, et qu'il y a stigmatisme rigoureux pour tous les points de la surface.
Donner un exemple de l'utilité de cette propriété.
Chercher l'image d'un point de la surface du dioptre.
Aide simple
En tout point de la surface d'un dioptre séparant deux milieux d'indices absolus \(n_1\) et \(n_2\), on peut appliquer la loi de SNELL-DESCARTES \(\sin i_2=\frac{n_1}{n_2}\cdot\sin i_1\) et en déduire la relation d'ordre (< ou >) entre l'angle d'incidence \(i_1\) et l'angle de réfraction \(i_2\).
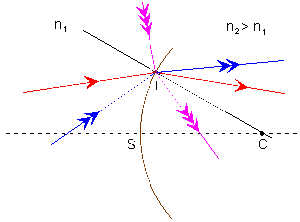
Considérez la trajectoire de plusieurs rayons incidents en un même point objet \(I\).
Rappel de cours
Le dioptre sphérique n'est rigoureusement stigmatique que pour les points de sa surface et son centre
Il y a stigmatisme approché pour tout point de l'espace qui n'envoie sur le dioptre sphérique qu'un pinceau lumineux dont le rayon moyen lui est normal, c'est à dire peu incliné par rapport à l'axe du dioptre ou encore formé de rayons paraxiaux.
Tout rayon incident parallèle à l'axe optique se réfracte en passant par le foyer image F'.
Un rayon incident passant par le foyer objet du dioptre se réfractera en un rayon parallèle à l'axe optique du dioptre.
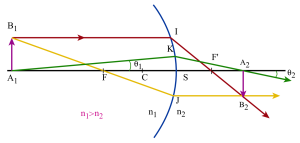
Pour construire l'image d'un objet plan :
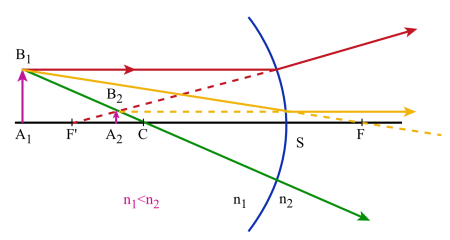
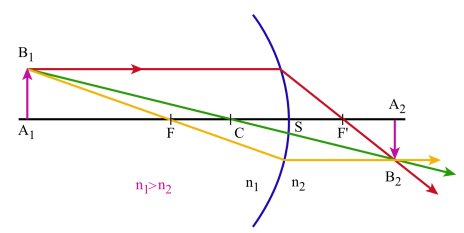
on utilise 3 rayons particuliers :
un rayon passant par le centre du dioptre et qui n'est pas dévié à la traversée de celui-ci
un rayon issu de \(B_1\) et passant par le foyer objet \(F\) : il est réfracté suivant une parallèle à l'axe principal
un rayon issu de \(B_1\) et parallèle à l'axe principal : il est réfracté suivant un rayon qui passe par le foyer image \(F'\).
Formules de conjugaison :
Origine au sommet
\(\frac{n_1}{\overline{SA_1}}.\frac{n_2}{\overline{SA_2}}=\frac{n_1-n_2}{\overline{SC}}\)
\(\gamma=\frac{n_1}{n_2}\frac{\overline{SA_2}}{\overline{SA_1}}\)
Origine au centre
\(\frac{n_1}{\overline{CA_2}}.\frac{n_2}{\overline{CA_1}}=\frac{n_1-n_2}{\overline{CS}}\)
\(\gamma=\frac{\overline{A_2B_2}}{\overline{A_1B_1}}=\frac{\overline{CA_2}}{\overline{CA_1}}\)
Origine aux foyers
\(\overline{FA_1}\overline{F'A_2}=\overline{SF}\overline{SF'}=ff'\)
\(\gamma=-\frac f{\overline{FA_1}}=\frac{\overline{F'A_1}}{f'}\)
Relation de Lagrange-Helmholtz :
Solution détaillée
Soit un point \(I\) quelconque de la surface du dioptre, quelle que soit la direction ou la longueur d'onde d'un rayon incident qui passe par \(I\), le rayon émergent conjugué de ce rayon incident passe également par \(I\). L'ensemble des rayons émergents, conjugués des rayons incidents contenant \(I\) ont un seul point commun : le point \(I\). Le point \(I\) est sa propre image par le dioptre.
Il y a donc stigmatisme rigoureux pour toutes les points de la surface d'un dioptre.
Le point d'incidence \(I\) d'un rayon quelconque sur la surface d'un dioptre sphérique est toujours confondu avec le point d'émergence \((I)\) du rayon émergent. Il en résulte que pour construire le rayon émergent du dioptre, il suffit d'un seul point image ou de la direction de ce rayon.