Étude de la fonction ln x
Cette partie comprend l'étude de la fonction \(\ln x\) et des fonctions composées \(\ln ~u(x)\) et \(\ln\arrowvert u(x)\arrowvert\) selon les rubriques suivantes :
Domaine de définition \(D_f\) de \(\ln x\) et Etude de \(\ln x\) aux bornes de \(D_f\)
Fonctions dérivées : \(\ln' (x)\) et \(\ln'' (x)\)
Tableau de variation et graphe de \(\ln x\)
Étude de la fonction composée : \(\ln u(x)\).
Étude de la fonction composée : \(\ln \arrowvert u(x)\arrowvert\).
Domaine de définition - Étude aux bornes
Domaine de définition \(D_f\) de \(\ln x\)
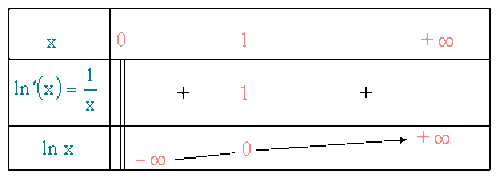
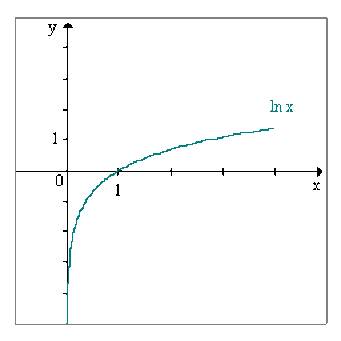
De par sa définition, la fonction ln est définie, dérivable (donc continue) et strictement croissante sur \(\mathbb{R}_{+}^{*}~ ( \ln'(x) = 1 / x >0 )\)
Etude de \(\ln x\) aux bornes de \(D_f\)
Démonstration :
\(\displaystyle{\lim_{x \to + \infty} \ln x = + \infty}\)
La fonction \(\ln x\) étant strictement croissante sur \(\mathbb{R}_{+}^{*}\) admet pour \(x\) tendant vers \(+\infty\) , une limite finie \(l\) ou une limite \(+ \infty\) .
Supposons l'existence d'une limite \(l\in\mathbb{R}\) quand \(x\) tend vers \(+ \infty\) alors :
\(\displaystyle{\lim_{x \to + \infty} \ln x \mapsto l \textrm{ et } \lim_{x \to + \infty} \ln(2x) \mapsto l}\)
or \(\ln (2x) = \ln 2 + \ln x \to \ln 2 + l \ne l\) car \(\ln 2\ne 0\) , ceci montre que
\(\displaystyle{\lim_{x \to +\infty} \ln x = + \infty}\)
Démonstration :
\(\displaystyle{\lim_{x \to + \infty} \frac{\ln x}{x} = 0}\)
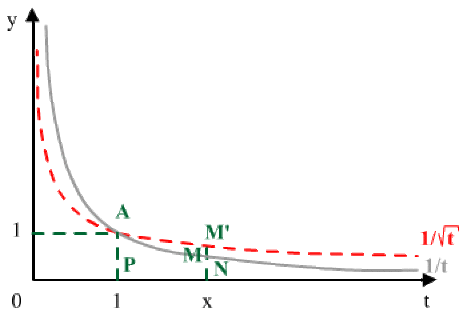
Pour \(x > 1\)
\(0< \textrm{Aire}(\textrm{PAMN}) < \textrm{Aire}(\textrm{PAM'N})\)
\(\displaystyle{0 < \ln x = \int_{1}^{x} \frac{\textrm{dt}}{\textrm{t}}<\int_{1}^{x} \frac{\textrm{dt}}{\sqrt{t}} = 2 \left(\sqrt{x} - 1\right) < 2 \sqrt{x}}\)
d'où
\(0 < \frac{\ln x}{x} < \frac{2}{\sqrt{x}}\)
On en déduit, à partir de cet encadrement[1], que
\(\displaystyle{\lim_{x \to +\infty} \frac{\ln x}{x} = 0}\)
La courbe représentative de la fonction \(\ln\) admet une branche parabolique dans la direction asymptotique \((x' x)\).
Démonstration :
\(\displaystyle{\lim_{x \to 0^{+}} \ln x = - \infty}\)
Posons \(X = 1 / x\) avec \(X \to \infty\) quand \(x \to 0^{+}\) , d'où :
\(\displaystyle{\lim_{x \to 0^{+}} \ln x = \lim_{X \to +\infty} \ln \frac{1}{X} = \lim_{X\to +\infty} \left[-\ln X\right] = - \infty}\)
La courbe représentative de la fonction \(\ln\) admet la droite d'équation \(x = 0\) (axe des ordonnées) comme asymptote.
Fonctions dérivées
Par définition : \(\ln' (x) = 1 / x > 0\) , \(\ln\) strictement croissante sur \(\mathbb{R}_{+}^{*}\).
Au point \(x = 1\) \(\ln' (1) = 1\) et la tangente à la courbe au point \((1,0)\) a pour coefficient directeur \(1\). Cette tangente est donc parallèle à la \(1\)ère bissectrice des axes dans un repère orthonormé. De plus, par définition de la dérivée de \(\ln\) en \(x = 1\) et du fait que \(\ln' (1) = 1\) nous avons :
\(\displaystyle{\lim_{x \to 1} \frac{\ln x - \ln 1}{x-1} = \lim_{x \to 1} \frac{\ln x}{x-1}} = \ln' (1) = 1\)
donc
\(\displaystyle{\lim_{x \to 1} \frac{\ln x}{x-1} = 1}\) ou \(\displaystyle{\lim_{X \to 0} \frac{\ln (1+X)}{X} = 1}\) (en posant \(X=x-1\))
D'où \(\ln (1+x) \sim x\) quand \(x \to 0\)
Par dérivation de \(\ln' (x)\) sur \(\mathbb{R}_{+}^{*}\) :
\(\ln''(x) = -\frac{1}{x^{2}}<0\)
\(\ln\) est concave sur \(\mathbb{R}_{+}^{*}\) .
Tableau de variation - Graphe
Fonction composée ln u(x)
Ensemble de définition \(D_f\)
La fonction \(f(x) = \ln(u(x))\) existe si \(u(x)\) existe et \(u(x) > 0\) d'où \(D_f = \{ x \in D_{u}~,~ u(x) > 0 \}\)
Exemple :
\(x \mapsto \ln \frac{x+1}{x-3}\) existe \(\Leftrightarrow x-3 \ne 0\) et \(\frac{x+1}{x-3}>0\)
d'où \(D_{u} = \{x \in \mathbb{R} - \{3\} \}\)
et \(D_{f} : x \in ] - \infty, -1[ \cup ]3 ; +\infty[\)
Limite de \(f\) aux bornes de \(D_f\)
Dans le cas d'une fonction composée si \(x_0\) est une borne de \(D_f\) :
si \(\displaystyle{\lim_{x \to x_{0}} u(x) = l}\)
alors : \(\displaystyle{\lim_{x \to x_{0}} \ln (u(x)) = \lim_{u(x_{0}) \to l} \ln ~u(x) = \left\{\begin{array}{llll} \ln l ~\textrm{ si }~ l \in \mathbb{R}_{+}^{\ast} \\ -\infty ~\textrm{ si }~ l = 0^{+} \\ +\infty ~\textrm{ si }~ l=+\infty \end{array}\right.}\)
Exemple :
\(f\) : \(x \mapsto \ln \frac{x+1}{x-3}\) est définie sur \(D_{f}\) : \(]-\infty, -1[ \cup ]3, +\infty[\)
Étude en \(-\infty\)
On a \(\displaystyle{\lim_{x \to -\infty}u(x) = \lim_{x \to - \infty} \frac{x}{x}=1}\)
soit \(X = \frac{x+1}{x-3}\)
donc \(\displaystyle{\lim_{x \to -\infty} \ln \frac{x+1}{x-3} = \lim_{X \to 1}~ \ln~ X = 0}\)
Étude en \(3^{+}\)
\(\displaystyle{\lim_{x \to 3^{+}} u(x) = + \frac{4}{0^{+}} = + \infty}\) donc \(\displaystyle{\lim_{x \to 3^{+}} \ln\left(\frac{x+1}{x-3}\right) = \lim_{X \to +\infty} \ln X = +\infty}\)
Etude semblable quand \(x \to -1^{-}\) et quand \(x \to +\infty\)
Dérivabilité de \(f\)
Si \(u(x)\) est dérivable sur \(D_f\) alors la fonction composée \(\ln \circ ~u\) est dérivable sur \(D_f\) et :
\(\forall x \in D_{f} \quad f'(x) = \ln' \left(u(x)\right) = \frac{u'(x)}{u(x)}\)
Exemple :
\(f\) : \(x \mapsto \ln \frac{x+1}{x-3}\) est définie sur \(D_{f} : ]-\infty ; -1[ \cup ]3 ; +\infty[\)
et comme la fonction rationnelle \(u(x) = \frac{x+1}{x-3}\) est dérivable sur \(\mathbb{R} - \{3\}\) , donc sur \(D_f\), on a :
\(\forall x\in D_{f} \qquad f'(x) = \frac{u'(x)}{u(x)}\)
or \(u'(x) = \frac{(x-3)-(x+1)}{(x-3)^{2}} = \frac{-4}{(x-3)^{2}}\)
donc
\(\forall x \in D_{f} \qquad f'(x) = \frac{-4}{(x-3)^{2}} \frac{(x-3)}{(x+1)} = \frac{-4}{(x-3)(x+1)}\)
Remarque :
Comme \(u(x) > 0\quad \forall x \in D_f , f '(x)\) a sur \(D_f\) le signe de \(u'(x)\) qui dans cet exemple est négatif.
Donc \(f'(x) < 0\) pour \(x \in ] - \infty ; -1 [ \cup ] 3; + \infty [\)
Fonction composée ln |u(x)|
Ensemble de définition \(D_{g}\)
La présence de la valeur absolue modifie le domaine de définition .
La fonction \(g(x) = \ln \arrowvert u(x)\arrowvert\) existe si \(u(x)\) existe et \(u(x) \ne 0\), d'où \(D_f = \{ x \in D_{u}, u(x) \ne 0 \}\)
Exemple :
\(x \mapsto \ln \left\arrowvert \frac{x+1}{x-3} \right\arrowvert\) existe \(\Leftrightarrow x-3 \ne 0\) et \(u(x) \ne 0 \Leftrightarrow x \ne -1\)
d'où \(D_{u} = \{ x \in \mathbb{R} - \{3\}\}\)
et \(D_g : x \in ] - \infty ; -1 [ \cup ] -1 ; 3 [ \cup ] 3; + \infty [\)
Limite de \(g\) aux bornes de \(D_g\)
En dehors de bornes supplémentaires et de la valeur absolue peu de modification dans l'étude des limites de \(g\) par rapport à celle de \(f\).
Dérivabilité de \(g\)
La valeur absolue ne modifie pas la fonction dérivée de \(\ln \arrowvert u(x)\arrowvert\).
En effet
\(\textrm{ si } u(x) > 0 \qquad g(x) = \ln ~u(x) ~\textrm{ et }~ g'(x) = \ln'(u(x)) = \frac{u'(x)}{u(x)}\)
\(\textrm{ si } u(x) < 0 \qquad g(x) = \ln \left[-u(x)\right] ~\textrm{ et }~ g'(x) = \ln'\left[-u(x)\right] = \frac{-u'(x)}{-u(x)} = \frac{u'(x)}{u(x)}\)
d'où
\(\forall x\in D_{g} \qquad g'(x) = \ln' \arrowvert u(x)\arrowvert = \frac{u'(x)}{u(x)}\)
Exemple :
\(g(x) = \ln \left \arrowvert \frac{x+1}{x-3} \right\arrowvert\)
\(\forall x \in D_{g} \qquad g'(x) = \frac{-4}{(x-3)(x+1)} \textrm{avec} \left\{\begin{array}{lll} g'(x)<0 \textrm{ si } x \in \left]-\infty ; -1 \right[ \cup \left]3 ; + \infty\right[ \\ g'(x) > 0 \textrm{ si } x \in \left]-1,3\right[ \end{array} \right.\)