Fonction logarithme de x, dans la base a
Définition :
On appelle fonction logarithme de base a \((a \in \mathbb{R}_{+}^{*}- \{1\})\) la fonction notée \(\log_{a}\) définie par : \(\forall x \in \mathbb{R}_{+}^{\ast} \quad \log_{a} x = \frac{\ln x}{\ln a}\)
Cas particuliers :
\(a = e\) : \(\log_{e} x = \frac{\ln x}{\ln e} = \ln x\) logarithme népérien
\(a = 10\) :\(\log_{10} x = \frac{\ln x}{\ln 10} = \log x\) logarithme décimal
sachant que \(\ln 10 \cong \mathrm{2,302}\) on en déduit que : \(\ln x \cong 2,30 \log x\) ou \(\log x \cong 0,43 \ln x\)
Propriété :
Propriétés des fonctions \(\log_{a}\) \((a \in \mathbb{R}_{+}^{\ast} - \{1\})\)
Elles se déduisent de celles du logarithme népérien.
\(\log_{a}\) est définie sur \(\mathbb{R}_{+}^{\ast}\)
\(\log_{a}\) est dérivable (donc continue) sur \(\mathbb{R}_{+}^{\ast}\) et
\(\forall x \in \mathbb{R}_{+}^{\ast} \quad \log_{a}'(x) = \frac{1}{x \ln~ a}\)
\(\log_{a}1 = 0\)
\(\forall(x,y) \in \left(\mathbb{R}_{+}^{\ast}\right)^{2} \qquad \log_{a} (xy) = \log_{a} x + \log_{a} y\)
\(\forall(x,y) \in \left(\mathbb{R}_{+}^{\ast}\right)^{2} \qquad \log_{a} \left(\frac{x}{y}\right) = \log_{a} x - \log_{a} y\)
\(\forall y \in \mathbb{R}_{+}^{\ast} \qquad \log_{a}\left(\frac{1}{y}\right) = - \log_{a} y\)
\(\displaystyle{\forall n \in \mathbb{N}^{\ast}, \forall x_{i} \in \mathbb{R}_{+}^{\ast} \quad \log_{a} \left(\prod_{i=1}^{n} x_{i}\right) = \sum_{i=1}^{n} \log_{a} x_{i}}\)
\(\forall n \in \mathbb{Q}, \forall x \in \mathbb{R}_{+}^{\ast} \quad \log_{a} \left(x^{n}\right) = n \log_{a} x\)
Etude des fonctions \(\log_{a}\) \((a \in \mathbb{R}_{+}^{\ast} - \{1\})\)
Les propriétés des fonctions \(\log_{a}\) dépendent de la position de a par rapport à \(1\).
1er cas : \(0 < a < 1\) , \(\ln ~a < 0\) (Comportement de \(\log_{a}\) contraire à la fonction \(\ln\))
Domaine de définition : \(D_f =R_{+}^{*}\)
Etude aux bornes de \(D_{f}\) :
Quand \(x \to + \infty \quad \ln x \to + \infty ~\ln a<0 ~\textrm{ et }~\displaystyle{\lim_{x\to +\infty} \log_{a} x= -\infty}\)
( Branche parabolique de direction asymptotique \(x'x\) )
Quand \(x \to 0^{+} \quad \ln x \to - \infty ~\ln a<0 ~\textrm{ et }~\displaystyle{\lim_{x\to 0^{+}} \log_{a} x= +\infty}\)
( Asymptote verticale d'équation x = 0 )
Fonctions dérivées
\(\log_{a}'(x) = \frac{1}{x \ln a}<0 \quad \log_{a} x\) est strictement décroissante sur \(\mathbb{R}_{+}^{\ast}\)
\(\log_{a}''(x) = \frac{-1}{x^{2}\ln a} >0 \quad \log_{a} x\) est convexe sur \(\mathbb{R}_{+}^{\ast}\)
Tableau de variation et graphe
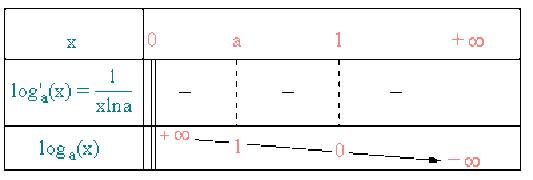
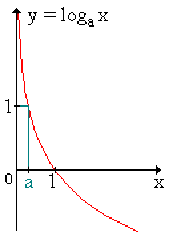
2ème cas : \(a > 1\) , \(\ln ~a > 0\) (Comportement de \(\log_{a}\) semblable à la fonction \(\ln\) car \(\ln = \log_{e}\) avec \(e >1\))
Domaine de définition : \(D_f = R_{+}^{\ast}\)
Etude aux bornes de \(D_f\) :
Quand \(x \to + \infty \quad \ln x \to + \infty ~\ln a>0 ~\textrm{ et }~\displaystyle{\lim_{x\to +\infty} \log_{a} x= +\infty}\)
( Branche parabolique de direction asymptotique \(x'x\) )
Quand \(x \to 0^{+} \quad \ln x \to - \infty ~\ln a>0 ~\textrm{ et }~\displaystyle{\lim_{x\to 0^{+}} \log_{a} x= -\infty}\)
( Asymptote verticale d'équation x = 0 )
Fonctions dérivées
\(\log_{a}'(x) = \frac{1}{x \ln a}>0 \quad \log_{a} x\) est strictement croissante sur \(\mathbb{R}_{+}^{\ast}\)
\(\log_{a}''(x) = \frac{-1}{x^{2}\ln a} <0 \quad \log_{a} x\) est concave sur \(\mathbb{R}_{+}^{\ast}\)
Tableau de variation et graphe
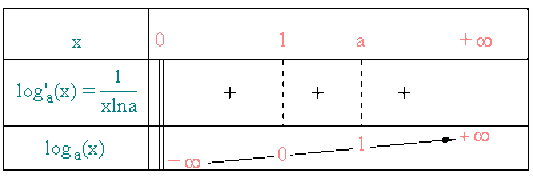
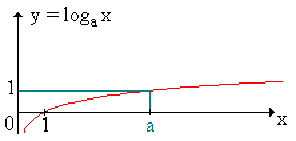
Changement de base
\(\forall (a,b) \in [ \mathbb{R}_{+}^{\ast}-\{1\} ]^{2}\) , on peut exprimer le \(\log_{b} x\) en fonction de \(\log_{a} x\) pour \(x \in \mathbb{R}_{+}^{\ast}\)
Par définition :
\(\log_{b} x = \frac{\ln x}{\ln b} \textrm{ et } \log_{a}x = \frac{\ln x}{ \ln a}\)
d'où \(\log_{b} x = \frac{\ln x}{\ln b} = \frac{\ln a}{\ln b} \log_{a} x\)
sachant que \(\frac{\ln a}{\ln ~b} = \log_{b} a = \frac{1}{\log_{a} b}\)
nous obtenons \(\log_{b}x = \log_{b}a \times \log_{a}x = \frac{\log_{a}x}{\log_{a}b}\)
Exemple :
\(\log_{3}x = \log_{3}9 \times \log_{9}x = \frac{\ln 9}{\ln 3} \times \log_{9} x = 2 \log_{9}x\)