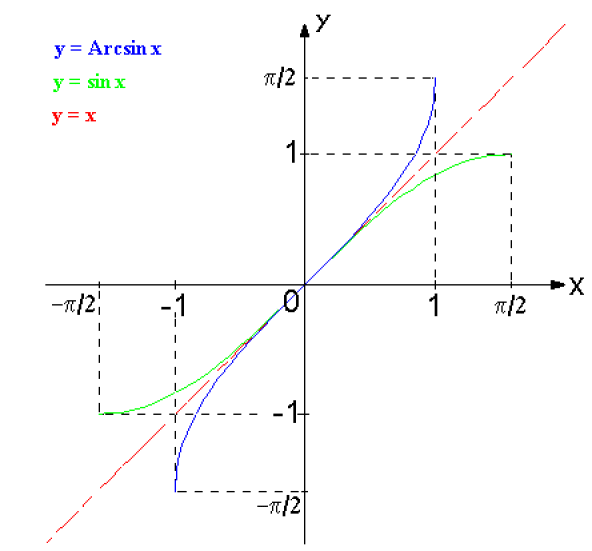
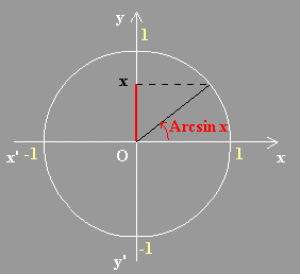
Fonction Arcsinus de x : Arcsin x
Définition :
L'application \(\sin\) : \([-\pi/2 ,~ \pi/2] \to [-1, 1]\) continue et strictement croissante admet une fonction réciproque notée \(\sin^{-1}\) ou \(\textrm{Arcsin}\) : \([-1, 1] \to [-\pi/2 , \pi/2]\)
\(y = \textrm{Arcsin }x \Leftrightarrow x = \sin y\)
\(x\in[-1,1] \textrm{ et } y \in \left[-\frac{\pi}{2}, + \frac{\pi}{2}\right]\)
\(\begin{array}{llll} \sin (\textrm{Arcsin }x) = x & \forall x \in[-1,1] \\ \cos (\textrm{Arcsin }x) = \sqrt{1-x^{2}} & \forall x \in[-1,1]\\\tan (\textrm{Arcsin }x) = \frac{x}{\sqrt{1-x^{2}}} & \forall x \in]-1,1[\\\textrm{cotan }(\textrm{Arcsin }x) = \frac{\sqrt{1-x^{2}}}{x} & \forall x \in[-1,0[ \cup]0,1]\end{array}\)
fonction impaire, d'où une étude sur \(D_{e} = [0,1]\).
fonction dérivable sur \([0,1[\) et :
\(\textrm{Arcsin }' x = \frac{1}{\sin'(\textrm{Arcsin }x)} = \frac{1}{\cos(\textrm{Arcsin }x)} = \frac{1}{\sqrt{1-x^{2}}}>0\)
donc fonction croissante sur \([0,1[\).
tableau de variation :
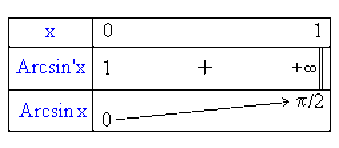
Représentation graphique de Arcsin x
