Régime transitoire et régime forcé
Durée : 10 mn
Note maximale : 8
Question
On considère un oscillateur harmonique en régime forcé. Il s'agit d'un oscillateur mécanique décrit par la figure ci-dessous.
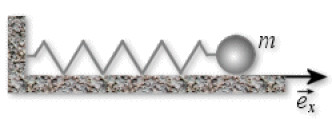
L'expression analytique de la position\(x\), au cours du temps\(t\), s'exprime par la fonction suivante :\(x(t) = x_{m}e^{-\lambda t}\cos(\omega_{1}t + \varphi) + x_{pm}\cos(\Omega t + \Phi)\)
\(\lambda\)représente le coefficient d'amortissement,\(x_{m}\)et\(x_{pm}\),\(\omega_{1}\)et\(\Omega\),\(\varphi\)et\(\Phi\)représentent respectivement les amplitudes, les pulsations et les phases à\(t = 0\)des deux fonctions (\(x_{g}(t)\)et\(x_{p}(t)\)) formant\(x(t)\).
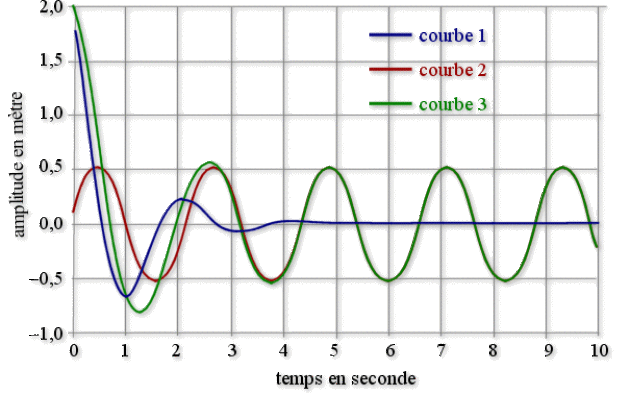
L'analyse de la réponse de l'oscillateur conduit au tracé des courbes représentées dans la figure ci-dessous :
Indiquer à quelles fonctions correspond chacune des courbes. (2 pts)
Quels sont les intervalles de temps correspondant aux régimes transitoire et permanent ? (1 pt)
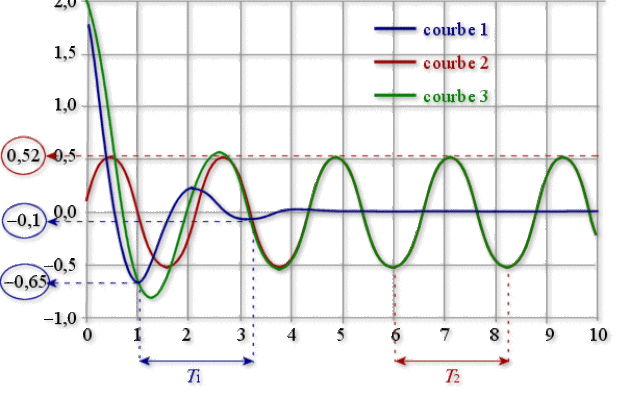
Déterminer graphiquement les valeurs numériques\(T_{1}\)(pseudo-période) et\(\delta\)(décrément logarithmique). En déduire les valeurs de la pseudo-pulsation et du coefficient d'amortissement. (3 pts)
Déterminer graphiquement les valeurs de l'amplitude et de la pulsation des oscillations en régime permanent. En déduire la valeur de la pulsation de l'excitation. (2 pts)
Solution
1. (2 pts)
La courbe 2 est une sinusoïde parfaite. Elle correspond donc à\(x_{pm}\cos(\Omega t + \Phi)\).
La courbe 1 est une sinusoïde amortie. Elle correspond donc à\(x_{m}e^{-\lambda t} \cos(\omega_{1}t + \varphi)\).
La courbe 3 est la somme des courbes 1 et 2. Elle correspond donc à\(x(t)\).
2. (1 pt)
Le régime permanent est défini pour\(x(t) \approx x_{p}(t)\)alors que le régime transitoire est défini pour\(x(t) = x_{g}(t) + x_{p}(t)\).
Ainsi, à partir de la figure on voit que le régime permanent est atteint pour\(t = 4\textrm{s}\). On a donc :
\(\begin{array}{rrrrr} 0< t <4 \textrm{ s} & \Rightarrow & \textrm{r\'egime transitoire} \\ t > 4\textrm{ s} & \Rightarrow & \textrm{r\'egime permanent} \end{array}\)
3. (3 pts)
La figure montre qu'à partir de la courbe 1, il est possible de mesurer la pseudo-période :
\(T_{1} = \mathrm{3,2} - 1 = \mathrm{2,2}\textrm{s}\)
Par conséquent,\(\omega_{1} = \frac{2\pi}{\mathrm{2,2}} = \mathrm{2,85}\textrm{ rad.s}^{-1}\)
Pour mesurer le décrément logarithmique, on mesure par exemple les amplitudes de 2 minima successifs de la sinusoïde amortie (courbe 1) et on a :
pour le premier minimum :\(-\mathrm{0,65}\)
pour le deuxième minimum :\(-\mathrm{0,1}\)
Par conséquent, on a :\(\qquad\) \(\delta = \ln\frac{-\mathrm{0,65}}{-\mathrm{0,1}} \approx \mathrm{1,9}\)
On en déduit alors le coefficient d'amortissement\(\lambda\)par la relation :
\(\qquad\) \(\lambda = \frac{\delta}{T_{1}} = \frac{\mathrm{1,9}}{\mathrm{2,2}}\approx\mathrm{0,9}\textrm{rad.s}^{-1}\)
4. (2 pts)
L'amplitude des oscillations en régime permanent est mesurée à partir de la courbe 2, et on a :
\(x_{pm} = \mathrm{0,52}~\textrm{m}\)
On détermine la période des oscillations à partir de la courbe 3 :
\(T_{2} = \mathrm{8,2} - 6 = \mathrm{2,2}\textrm{s}\Rightarrow \Omega = \frac{2\pi}{T_{2}} = \frac{2\pi}{\mathrm{2,2}} = \mathrm{2,85}\textrm{ rad.s}^{-1}\)
La pulsation des oscillations de l'excitation n'est autre que la pulsation que nous venons de calculer\(\Omega\)puisqu'on est en régime permanent.