Exploitation graphique
Durée : 5 mn
Note maximale : 4
Question
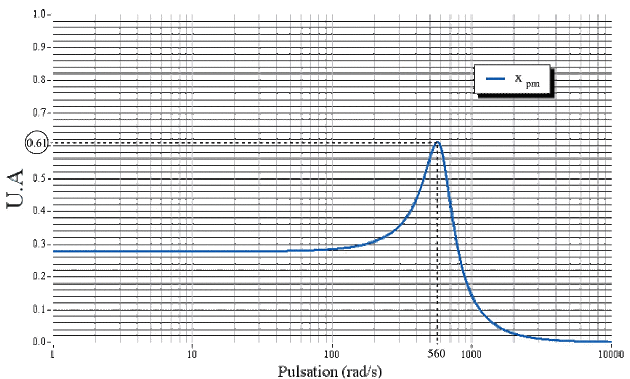
On considère la courbe de résonance suivante :
Déterminer la pulsation de résonance\(\Omega_{r}\). (1 pt)
Rappeler la définition puis déterminer la bande passante\(\Delta\Omega\). (2 pts)
Dans le cas où l'amortissement est très faible, quelle est la signification du rapport entre la pulsation de résonance et la bande passante\(\frac{\Omega_{r}}{\Delta\Omega}\) . (1 pt)
Solution
1. (1 pt) La pulsation de résonance est localisée au pic comme le montre la figure suivante :
Sa valeur est égale à : \(\Omega_{r} = 560\textrm{rad.s}^{-1}\)
Remarque :
On fera attention à l'échelle des pulsations du graphique puisque celle-ci est logarithmique.
2. (2 pts) La bande passante\(\Delta\Omega\)est définie par les deux pulsations\(\Omega_{1}\)et\(\Omega_{2}\)telle que
\(\Delta\Omega = \Omega_{1} - \Omega_{2}\), où\(\Omega_{1}\)et\(\Omega_{2}\)vérifient :
\(x_{pm}(\Omega_{1}) = x_{pm}(\Omega_{2}) = \frac{x_{pm}(\Omega_{r})}{\sqrt{2}}\)
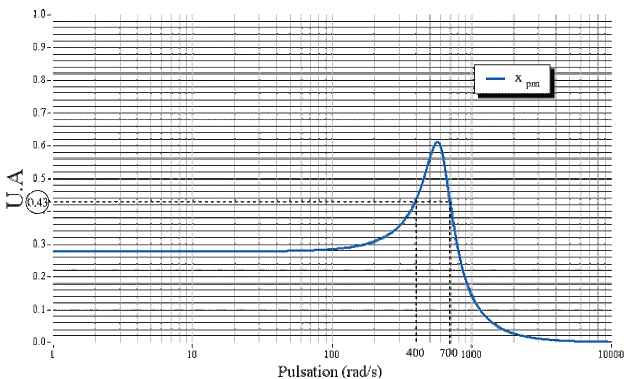
Graphiquement, on détermine\(x_{pm}(\Omega_{r}) = \mathrm{0,61}\). Par conséquent, \(\frac{x_{pm}(\Omega_{r})}{\sqrt{2}} = \mathrm{0,43}\). On trouve\(\Omega_{1} = 400\textrm{rad.s}^{-1}\)et\(\Omega_{2} = 700\textrm{rad.s}^{-1}\)comme le montre la figure suivante :
La bande passante est donc égale à :\(\qquad\) \(\Delta\Omega = 300\textrm{rad.s}^{-1}\)
3. (1 pt) Lorsque l'amortissement\(\lambda\)est très faible, on montre que\(\Delta\Omega \approx 2\lambda\)c'est-à-dire que la bande passante est très étroite, ce qui signifie que\(\frac{\Omega_{r}}{\Delta\Omega}\)est très grand.