Le modèle de Hardy-Weinberg

Soient \(A\) et \(a\) 2 allèles à un même gène, de fréquences respectives p et q, avec \(A\) dominant sur \(a\). Dans ce cas les génotypes (\(AA\)) et (\(Aa\)) ne pourront pas être distingués dans la population.

Seuls les individus de phénotype [\(A\)] d'effectif N1 pourront être reconnus des individus de phénotypes [\(a\)] d'effectif N2.

avec : \(q^{2} = \frac{N_{2}}{N} = \frac{N_{2}}{N_{1} + N_{2}}\)

et la fréquence de l'allèle : \(a = f(a) = \sqrt{q^{2}} = \sqrt{\frac{N_{2}}{N_{1} + N_{2}}}\)

Il s'agit d'une méthode couramment utilisée en génétique humaine pour calculer la fréquence des gènes récessifs rares.

Fréquences des homozygotes et des hétérozygotes pour des gènes récessifs rares chez l'homme (d'après Lenz, 1976) :

La figure 1 (ci-dessous) montre la correspondance entre la fréquence allélique q de M et les fréquences génotypiques dans le cas de deux allèles en régime panmictique. Lorsque l'un des allèles est rare, presque tous se trouvent dans la population sous la forme hétérozygote.

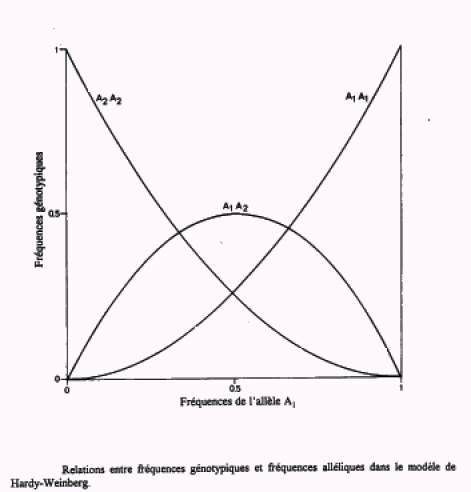
La fréquence maximale des hétérozygotes H est atteinte lorsque : \(p = q\) et \(H = 2pq = 0,50\)

Bien que le système des groupes sanguins (ABO) chez l'homme soit souvent pris comme un exemple simple de polyallélie, il représente cependant un cas relativement complexe à cause de la codominance de \(I^{A}\) et \(I^{B}\), de la présence d'un allèle nul \(i^{0}\) et de la dominance de \(I^{A}\) et \(I^{B}\) sur \(i^{0}\).

Si l'on désigne par :

• p la fréquence de l'allèle \(I^{A}\),

• q la fréquence de l'allèle \(I^{B}\),

• r la fréquence de l'allèle \(i^{0}\),

avec (\(p + q + r = 1\)),

les diverses fréquences génotypiques et phénotypiques sont observées en appliquant la loi de Hardy-Weinberg.

En utilisant les identités remarquables

telles que :

• \(p^{2}+2pr+r^{2} = (p+r)^{2}\)

• \(q^{2}+2qr+r^{2} = (q+r)^{2}\)

avec :

• f [A] + f [O] = \((p+r)^{2}\)

• f [B] + f [O] = \((q+r)^{2}\)

• et f[O] = \(r^{2}\)

ainsi :

• \(r = \sqrt{F [O]}\) et \(q = \sqrt{F [B] + F [O]}^{-r}\)

• \(p = 1 - \sqrt{F [O] + F [B]}\) et \(q = 1 - \sqrt{F[O] + F[A]}\)

• \(p = \sqrt {F[A] + F[O]} -r\)

  OR, \(p + q + r = 1\)

• Ce sont les formules de Bernstein (1930)

Si le mâle est hétérogamètique (comme pour l'homme), soit A un gène situé sur le chromosome X et présent sous 2 formes allèliques : \(A_{1}(p)\) et \(A_{2}(q).\)

Si Hardy-Weinberg

Dans le cas où on a 1 locus autosomique, l'équilibre de Hardy Weinberg est obtenu en 1 génération de croissance au hasard.

Si 1 locus est lié au sexe, Hardy-Weinberg est atteint de manière asymptotique au bout de 8-10 générations.

1. Hardy-Weinberg pour un gène hétérosomal (gonosomique)

2. Chromosome Y : fréquence p et q chez le sujet XY ; transmission aux descendants mâles

3. Chromosome X : soit \(q_{x}\) chez l'homme, et \(q_{xx}\) chez la femme, fréquence de l'allèle q

L'X des garçons (de génération n) est transmis par les mères (génération n-1) → \(q_{x}^{(n)} = q_{xx}^{(n-1)}\)

L'X portant l'allèle q des filles a :

• \(\frac{1}{2}\) chance de venir du père

• \(\frac{1}{2}\) chance de venir de la mère \(q_{xx}^{n} = \frac{q_{x}^{(n-1)} + q_{x}^{(n-1)}}{2}\)

\rightarrow \textrm{Fréquence de l'allèle chez l'homme = fréquence chez la femme à la génération précédente}

\rightarrow \textrm{Fréquence de l'allèle chez la femme = moyenne des fréquences des 2 sexes à la génération précédente}

Calcul de la différence des fréquences alllèliques entre les 2 sexes :

\(q_{x}^{n} - q_{xx}^{n} = q_{xx}^{n-1} - \frac{q_{x}^{n-1} + q_{x}^{n-1}}{2} = \frac{1}{2}~(q_{x}^{n-1} - q_{x}^{n-1})\)

\(\rightarrow q_{x}^{n} - q_{xx}^{n} = (\frac{-1}{2})^{n}(q_{xx}^{0} - q_{xx}^{0})\) : tend vers zéro en 8 à 10 générations.

fréquence moyenne q :

• 1/3 des X appartenant à l'homme , 2/3 à la femme : q = 1/3 qx(n) + 2/3 qx x (n)

• la fréquence moyenne invariante (développer q1 en q0 ... \(\rightarrow\) q1 - q0 )

• à l'équilibre, \(q^{(e)} \textrm{est :}~q_{xx}^{(e)} = q^{(e)}\)

Soient : Aa et Bb indépendants

f[AB] = p²r² + 2pqr² + 2p²rs + 4 pq rs

f[A] = p²s² + 2pqs²

f[B] = q²r² + 2p²rs

f[O] = q²s²