Calcul de la compacité dans le système cfc
Partie
Question
La compacité est le rapport du volume des atomes sur le volume de la maille.
Soit une maille cubique à faces centrées d'arête a contenant des atomes assimilés à des sphères tangentes de rayon R. La maille contient Z atomes.
Déterminer la compacité de cette maille.
Aide simple
Se reporter au cours pour comprendre le mode de construction du réseau cfc par empilement de plans compacts.
Le volume d'une sphère est \(\mathrm{V=\frac{4}{3}~\pi~R^3}\).
Aide méthodologique
Exprimer la compacité du cristal en fonction de Z, R et a.
Déterminer le nombre de groupements formulaires Z dans la maille.
Représenter la maille en identifiant un plan dans lequel les atomes sont tangents.
Déterminer la relation entre R et a, imposée par le fait que les sphères sont tangentes.
Solution détaillée
Soit V le volume d'un atome :
\(\mathrm{V=\frac{4}{3}~\pi~R^3}\)
La compacité s'exprime comme le rapport :
\(\mathrm{C=\frac{Z~V}{a^3}=\frac{4Z}{3}~\pi\left(\frac{R}{a}\right)^3}\)
La maille cfc est représentée ci-dessous. Les atomes sont tangents sur le plan indiqué sur la figure. Ce plan coupe trois faces suivant leur diagonale.
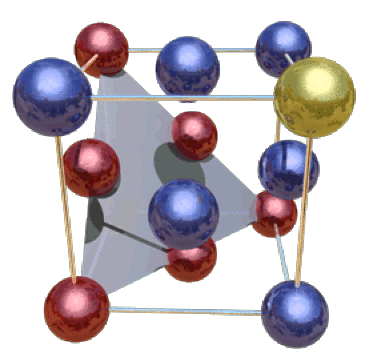
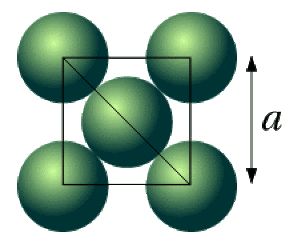
Sur la diagonale, de longueur \(\mathrm{a\sqrt2}\), on a :
\(\mathrm{a\sqrt2=4R}\) soit \(\mathrm{R=a~\frac{\sqrt2}{4}}\)
Dans la maille, chaque atome situé sur un sommet compte pour un huitième. Il y a huit sommets. L'atome situé au centre d'une des six faces compte pour un demi. Le nombre de groupements formulaires est :
\(\mathrm{Z=8\times\frac{1}{8}+6\times\frac{1}{2}=4}\)
Le volume d'un atome est alors :
\(\mathrm{V=\frac{4}{3}~\pi~R^3=\frac{4}{3}\pi\left(\frac{a\sqrt2}{4}\right)^3=\frac{\sqrt2}{3\times8}~\pi~a^3}\)
La compacité est :
\(\mathrm{C=\frac{Z~V}{a^3}=4\times\frac{\sqrt2}{3\times8}\pi~a^3\times\frac{1}{a^3}=\frac{\sqrt2}{6}\pi=0,74}\)