Calcul de la compacité dans le système hexagonal compact
Partie
Question
Soient trois mailles de type hexagonal compact représentées ci-dessous, contenant des atomes assimilés à des sphères tangentes de rayon R. La maille contient Z atomes. Les paramètres de maille sont a et c.
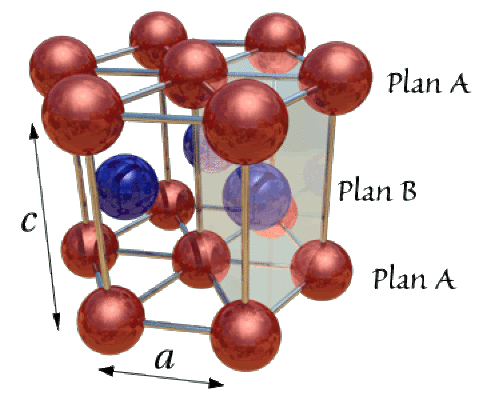
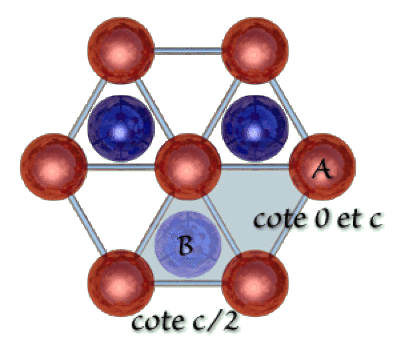
Dans le système hexagonal compact, on montre que c et a sont liés par la relation :
\(\frac{\mathrm{c}}{\mathrm{a}}=1,633\)
Déterminer la compacité de cette maille.
Aide simple
Le volume d'une sphère est \(\mathrm{V=\frac{4}{3}\pi~R^3}\).
La base de la maille est un losange. Le grand angle vaut 120°. Ce losange est composé de deux triangles équilatéraux de côté a.
Aide méthodologique
Déterminer le volume de la maille en fonction du paramètre a.
Déterminer le nombre de groupements formulaires Z dans la maille.
Représenter la maille en identifiant un plan dans lequel les atomes sont tangents.
Déterminer la relation entre R et a, imposée par l'empilement compact.
Solution détaillée
Le volume de la maille hc est le produit de la hauteur par la surface de la base.
La hauteur c est égale à \(\mathrm{c=1,633~a}\)
La surface de la base vaut deux fois la surface d'un triangle équilatéral de côté.a.
C'est aussi la surface d'un rectangle de côtés a et\( \mathrm{a}\sin(120°)\) représenté ci-dessous.

La surface du losange est donc :
\(\mathrm{S=a^2\sin(120°)=\frac{\sqrt3}{2}a^2}\)
et le volume de la maille est :
\(\mathrm{v=S~c=1,633\frac{\sqrt3}{2}a^3}\)
Sur la base de la maille représentée ci-dessous les atomes sont tangents sur l'arête. Il vient alors \(\mathrm{a=2R}\)
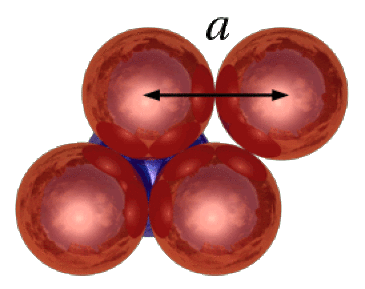
Soit V le volume d'un atome. Il vient donc :
\(\mathrm{V=\frac{4}{3}\pi~R^3=\frac{4}{3}\pi\left(\frac{a}{2}\right)^3=\frac{\pi}{6}a^3}\)
Dans la maille, chaque atome situé sur un sommet compte pour un huitième. Il y a huit sommets. L'atome situé à l'intérieur de la maille compte pour un. Le nombre de groupements formulaires est :
\(\mathrm{Z=8\times\frac{1}{8}+1\times1=2}\)
La compacité s'exprime comme le rapport :
\(\mathrm{C=\frac{Z~V}{v}=2\times\frac{\pi}{6}a^3\times\frac{2}{1,633\sqrt3~a^3}=\frac{2\pi}{3\times1,633\times\sqrt3}=0,74}\)
On retrouve la compacité maximale d'un empilement compact. C'est la même valeur que pour l'empilement cfc.