Définition d'une suite de nombres réels, exemples
Définition : Suite réelle
Une suite de nombres réels (ou suite de réels ou suite réelle) est une application de \(\mathbb N\) dans \(\mathbb R\).
\((u_n) :\mathbb N\to\mathbb R\quad n\mapsto u_n\)
Attention : Notations
On note :
\( u_n\) et non \(u(n)\) l'image de \(n\), c'est le terme d'indice \(n\),
\((u_n)_{n\in\mathbb N}\) ou \((u_n)\) la suite c'est à dire l'application de \(\mathbb N\) dans \(\mathbb R\), c'est un élément de l'ensemble (\(\mathbb N, \mathbb R\)), noté encore \(\mathbb R^{\mathbb N}\),
\(\{u_n,n\in\mathbb N\}\) l'ensemble des valeurs prises par la suite \((u_n)\).
Ainsi la suite\( ((-1)^n)\) ne prend que deux valeurs 1 et -1, \(\{u_n,n\in\mathbb N\}=\{-1,+1\}\) alors qu'elle a bien évidemment une infinité de termes.
Eventuellement une suite peut être définie seulement à partir d'un certain rang \(n_0\) ainsi les suites :
\(\displaystyle{\left(\frac{1}{n(n-2)}\right)_{n\geq 3},\left(\sqrt{n-7}\right)_{n\geq 7}}\)
Une suite peut être définie de plusieurs manières, les plus fréquentes sont les suivantes :
1. Suite définie explicitement
\((u_n)\) est définie par une formule .
\(\displaystyle{u_n=f(n)}\)
On calcule directement \(u_n\) en fonction de \(n\).
Exemple :
Parmi les suites de référence citons:
Suites arithmétiques : ce sont les suites \((a+nr),a\in\mathbb R,r\in\mathbb R\).
Suites géométriques : ce sont les suites \((ak^n),a\in\mathbb R,k\in\mathbb R\)
Suites puissances : ce sont les suites \(( n^{\alpha})_{n\geq 1},\alpha\in\mathbb R\)
Certaines suites sont définies par une formule où interviennent un nombre de termes dépendant de \(n\) comme la suite \((u_n)\) définie par \(\displaystyle{u_n=\frac{1}{n+1}+\frac{1}{n+2}+\cdots+\frac{1}{2n}}\).
Les représentations :
Pour représenter une suite définie explicitement deux points de vue sont donc possibles :
une représentation "axiale", les termes successifs de la suite sont représentés sur un axe;
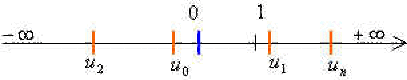
une représentation graphique, on trace le graphe de l'application \((u_n)\) de \(\mathbb N\) dans \(\mathbb R\) c'est-à-dire l'ensemble des points \((n, u_n), n\in\mathbb N\).
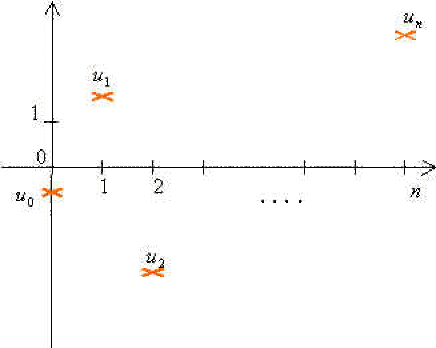
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
b. Suite définie par une relation de récurrence
\((u_n)\) est définie par une relation de récurrence
\(\displaystyle{\forall n\in\mathbb N,u_{n+1}=\phi(u_{n})}\)
et la donnée de \(u_0\), \(\phi\) désigne une fonction réelle de variable réelle.
Ces suites seront étudiées plus particulièrement dans la suite, mais nous considérerons le long de ce chapitre une suite "test" la suite, que nous noterons \(\mathcal U\), définie par :
\(\left\{\begin{array}{ll}u_0=2, &\\ u_{n+1}=\frac{u_{n}}{2}+\frac{1}{u_{n}} & \forall n\in \mathbb N\end{array}\right.\)
On ne calcule pas directement \(u_n\) , on a à sa disposition un algorithme.
Cet algorithme permet, pour tout entier \(n\), de calculer les \(n\) premiers termes de la suite.
L'algorithme peut être schématisé, dans ce cas, par une représentation graphique, par exemple dans le cas de la suite \(\mathcal U\) définie comme précédemment:
Pour une meilleure illustration, nous proposons les deux exemples suivants:
Exemple :
1. \({\left\{\begin{array}{ll}u_0=1,8 &\\u_{n+1}=\sqrt{u_n} & \forall n\in\mathbb N\end{array}\right.}\)
2. \({\left\{\begin{array}{ll}u_0=0,2 &\\u_{n+1}=\sqrt{u_n} & \forall n\in\mathbb N\end{array}\right.}\)
Attention :
Si \(\phi\) est définie sur un intervalle \(I\) de \(\mathbb R\), distinct de \(\mathbb R\), il faut éliminer les valeurs de \(u_0\) telles que, pour un entier \(p\), \(u_p\) n'appartient pas à \(I\), en effet \(u_{p+1}\) n'est alors pas défini. Le problème de la définition de la suite est bien évidemment le premier qu'on doit se poser.
Exemple :
Si \(\phi\) est la fonction \(\displaystyle{x\mapsto\frac{1}{x+2}}\) il faut éliminer \(-2\) mais aussi \(-\frac{5}{2}\) car si \(u_0 =-\frac{5}{2}, u_1 = -2\) et on ne peut plus calculer \(u_2\). On élimine de même \(-\frac{12}{5}\), ...
Soit le cas de la suite\( \mathcal U\), définie par :
\({\left\{\begin{array}{ll}u_0=2, &\\u_{n+1}=\frac{u_n}{2}+\frac{1}{u_n} & \forall n\in\mathbb N\end{array}\right.}\)
On remarque que la fonction \(\phi\) satisfait à la condition :
\(\displaystyle{\forall x\in]0,+\infty[,\phi(x)>0}\) ,
il n'y a donc pas de problème de définition.
Dans certains cas on passe facilement de la forme récurrente à la forme explicite et inversement, c'est le cas pour les suites arithmétiques et géométriques.
la forme récurrente d'une suite arithmétique est : \({\left\{\begin{array}{ll}u_0=a, &\\u_{n+1} - u_n=r & \forall n\in\mathbb N\end{array}\right.}\)
la forme récurrente d'une suite géométrique est : \({\left\{\begin{array}{ll}u_0=a, &\\u_{n+1}=ku_n & \forall n\in\mathbb N\end{array} \right.}\)
Eventuellement, on considère des suites définies par une relation de récurrence d'ordre 2 :
\({\left\{\begin{array}{ll}u_0, &\\u_1, &\\u_{n+2}=\phi(u_{n+1},u_n) & \forall n\in\mathbb N\end{array}\right.}\)
\(\phi\) est alors une fonction réelle définie sur une partie de \(\mathbb R^2\).
C'est le cas des suites de Fibonacci, vues dans l'introduction, la fonction \(\phi\) est alors la fonction:
\(\displaystyle{\phi :\mathbb R^2\to\mathbb R\quad(x,y)\mapsto x+y}\)