Théorème de Rolle
Dans tout ce paragraphe on considérera un intervalle fermé, borné \([a,b],(a< b)\).
Théorème : Rolle
Soit\( f\) une application de l'intervalle \([a,b]\) dans \(\mathbf R\) vérifiant les conditions suivantes :
\(f\) est continue sur \([a,b]\),
\(f\) est dérivable sur \(]a,b[\) ,
\(f(a)=f(b)\)
Alors il existe \(c\in]a,b[\) tel que\( f'( c ) = 0\).
Complément : Interprétation
Grâce aux hypothèses, le graphe de la fonction admet une tangente en tout point de \(]a,b[\) et il joint deux points qui ont même ordonnée, le théorème affirme qu'il existe alors au moins un point à tangente horizontale.
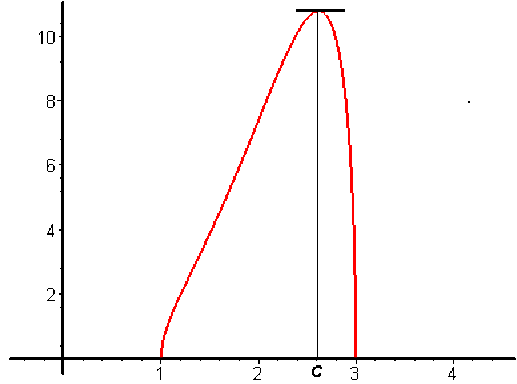
Remarquez que dans l'exemple ci-dessus \((a=1, b=3)\), la fonction est bien continue sur \([1,3]\) et dérivable sur \(]1,3[\) mais n'est dérivable ni en \(1\) ni en \(3\).
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Preuve :
La démonstration consiste à montrer que la fonction admet un extremum local en un point de \(]a,b[\).
Si \(\forall x\in[a,b]f(x)=f(a)\), on en déduit : \(\forall x\in~]a,b[,~f'(x)=0\).
Sinon, d’après la condition (1) la fonction, étant continue, est bornée, on pose : \(M=\underset{x\in[a,b]}{\textrm{sup}}f(x)\) et \(m=\underset{x\in[a,b]}{\textrm{inf}}f(x)\)
On a donc \(m < M\). Une, au moins, des inégalités strictes : \(M>f(a)\) ou \(m<f(a)\) est vérifiée.
On suppose qu’on a \(M > f (a)\).
La fonction \(f\) étant continue sur \([a,b]\), il existe \(c\in[a,b]\) tel que \(f(c)=M\), et \(c\) appartient à \(]a,b[\) car \(f(a)\ne M\) et \(f(b)\ne M\). La fonction \(f\) admet en \(c\) un maximum local. La fonction étant dérivable sur \(]a,b[\), on en déduit que \(f’(c) = 0\) (cf "extremum local et annulation de la dérivée" dans le module "Nombres réels, suites et fonctions").
Remarque : Remarque 1
Chacune des hypothèses est nécessaire :
les trois conditions
\(f\) est continue sur \([a,b]\)
\(f\) est dérivable sur \(]a,b[\) et
\(f(a) = f(b)\)
sont indispensables pour obtenir la conclusion ; les deux contre-exemples suivants le montrent pour les conditions 1 et 2, quant à la condition 3 sa nécessité est évidente.
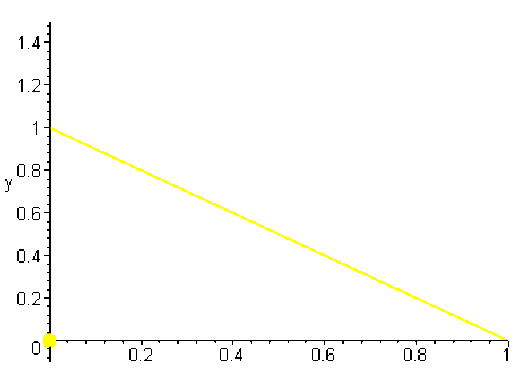
a. (continuité)
Soit \(\displaystyle{f :[0,1]\to \mathbf R, \forall x\in]0,1], f(x)=1-x}\) et \(f(0)=0\).
b.(dérivabilité)
Soit \(g :[-1,1]\to\mathbf R\quad x\mapsto\vert x\vert\).
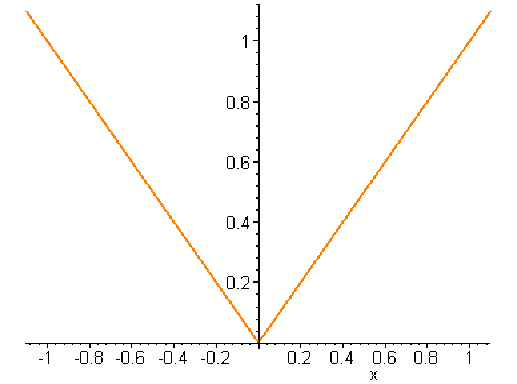
Remarque : Remarque 2
Le réel \(c\) n'est pas nécessairement unique comme le montre l'exemple de la fonction sinus sur \([0,2\pi]\) on a \(\displaystyle{f'\left(\frac{\pi}{2}\right)=f'\left(\frac{3\pi}{2}\right)=0}\).
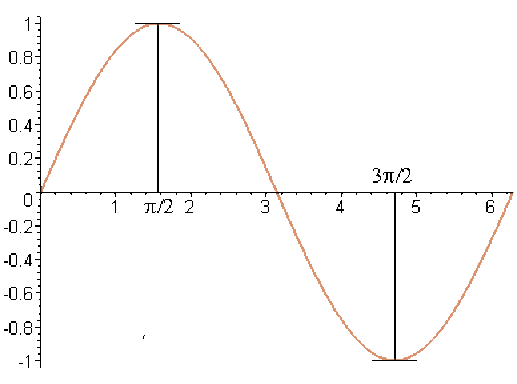
Remarque : Remarque 3
Application : les zéros de \(f'\) séparent les zéros de \(f\).
Le théorème énoncé par Rolle comporte la condition plus restrictive \(f(a)=f(b)=0\), cette dernière égalité n'est pas nécessaire à la démonstration mais ce théorème est souvent utilisé dans des problèmes de séparation des racines : il exprime en effet que, pour une fonction \(f\) dérivable, les zéros de \(f`\) séparent les zéros de \(f\) , c'est-à-dire qu'entre deux zéros de \(f'\) il y a au moins un zéro de \(f'\).
Exemple. Soit \(\mathcal P\) un polynôme à coefficients réels de degré \(n\) strictement positif ayant toutes ses racines réelles et distinctes, alors le polynôme dérivé a également toutes ses racines réelles et distinctes.
On note \(a_1< a_2<\cdots\cdots< a_n\) les racines de \(\mathcal P\), en appliquant le théorème de Rolle à la fonction polynôme \(x\mapsto\mathcal P(x)\) sur chacun des intervalles \([a_i,a_{i+1}](i=1,2\cdots n-1)\), on obtient que le polynôme dérivé \(\mathcal P'\) a au moins \(n-1\) racines réelles distinctes. Son degré étant \(n-1\), il en a au plus \(n-1\). D'où la conclusion.
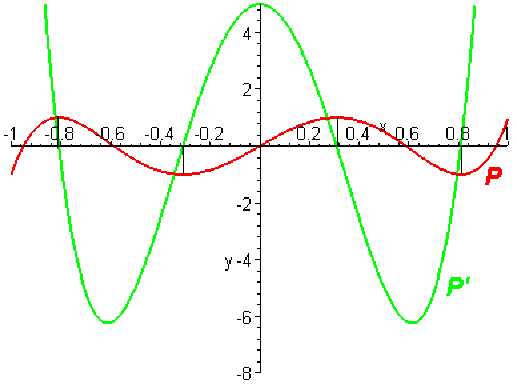
(Le graphe tracé est celui d'un polynôme de Tchebicheff et de sa dérivée).