Caractérisation de l'injectivité d'une fonction continue sur un intervalle
On considère les deux fonctions numériques \(f~\textrm{et}~g\)suivantes :
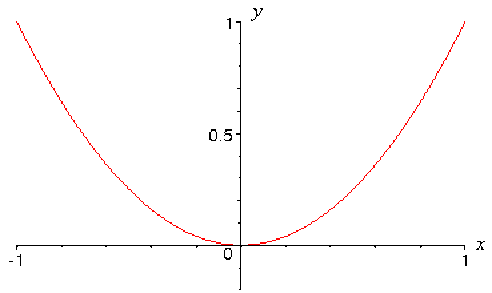
\(f : [-1, +1] \rightarrow \mathbb R \\ x \mapsto x^2x\)
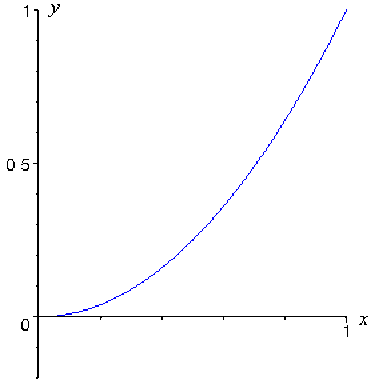
\(g : [0, +1] \rightarrow \mathbb R \\ x \mapsto x^2\)
Ces deux fonctions sont continues sur leurs intervalles de définition, mais \(f\) n'est pas injective alors que \(g\) est injective.
Ce qui différencie ces deux fonctions, c'est le fait que la fonction \(g\) est monotone sur son intervalle de définition alors que la fonction \(f\) ne l'est pas.
On a en fait la proposition suivante :
Proposition : Caractérisation de l'injectivité d'une fonction continue sur un intervalle
Soit \(f\) une fonction continue sur un intervalle.
1) Si \(f\) est strictement monotone, alors elle est injective
2) Si \(f\) est injective, alors elle est strictement monotone
Démonstration : Partie 1) de la proposition
\(f\) strictement monotone \(\Rightarrow f\) injective
On suppose par exemple que la fonction \(f\) est strictement croissante sur un intervalle \(I~de~\mathbb R\);
alors quels que soient les éléments distincts \(x~\textrm{et}~y~\textrm{de}~I,\) on a, comme \(\mathbb R\) est totalement ordonné,
soit \(x < y\) donc \(f(x) < f(y),\)
soit \(y < x\) donc \(f(y) < f(x),\)
dans les deux cas \(f(x)~\textrm{et}~f(y)\) sont distincts, ce qui est la définition de "\(f\) est injective".
Démonstration : Partie 2) de la proposition
\(f\) continue et injective \(\Rightarrow f\) strictement monotone
est plus complexe à établir.
Première étape
Soient \(u~\textrm{et}~v\) deux éléments de \(I\) vérifiant \(u < v\)(rappel : \(I\) n'est ni vide ni réduit à un point).
Comme \(f\) est injective et \(\mathbb R\) totalement ordonné, on a soit \(f(u) < f(v),\) soit \(f(v) < f(u).\)
si \(f(u) < f(v),\) on montre que \(\forall x \in I, (u < x < v) \Rightarrow (f(u) < f(x) < f(v)).\)
On suppose donc \(f(u) < f(v)\) et soit \(x, u <x < v,\) (\(x\) est donc dans \(I\) puisque \(I\) est un intervalle).
On veut montrer que \(f(u) < f(x) < f(v).\)
On raisonne par l'absurde :
- si \(f(x) < f(u),\) on a donc \(f(x) < f(u) < f(v)\); or \(f\) est continue sur \(I\) donc sur l'intervalle \([x, v]\)contenu dans \(I\) ; donc d'après le "Théorème des valeurs intermédiaires", il existe un \(y\) appartenant à \(]x, v[\) tel que \(f(y)= f(u),\) or \(y\) est différent de \(u\) car on a \(u < x < y < v\); cela est en contradiction avec l'hypothèse \(f\) injective.
- si \(f(v) < f(x),\) on a \(f(u) < f(v) < f(x)\) et le même raisonnement conduit à dire qu'il existe un \(z\) dans \(]u, x[\) tel que \(f(z) = f(v),\) ce qui est aussi absurde.
si \(f(v) < f(u),\) on montre que \(\forall x \in I, (u < x < v) \Rightarrow f(v) < f(x) < f(u)),\) par un raisonnement identique au précédent, en intervertissant les rôles joués par \(f(u)~\textrm{et}~f(v)\)
On suppose donc \(f(v) < f(u)\) et soit \(x, u < x < v.\)
On veut montrer que \(f(v) < f(x) < f(u).\)
On raisonne par l'absurde :
- si \(f(x) < f(v),\) on a donc \(f(x) < f(v) < f(u)\); or \(f\) est continue sur \(I\) donc sur l'intervalle \([u, x]\)contenu dans \(I\) ; donc d'après le "Théorème des valeurs intermédiaires", 'il existe un \(z\) dans \(]u, x[\) tel que \(f(z) = f(v),\) or \(z\) est différent de \(v\) car \(u < z < x < v\); cela est en contradiction avec l'hypothèse \(f\) injective.
- si \(f(u) < f(x),\) on a \(f(v) < f(u) < f(x)\) et le même raisonnement conduit à dire qu'il existe un \(y\) appartenant à \(]x, v[\) tel que \(f(y) = f(u),\) ceci est aussi absurde.
Deuxième étape
On montre que quels que soient les éléments \(a~\textrm{et}~b~\textrm{de}~I\) vérifiant \(a < b,\) la fonction \(f\) est strictement monotone sur \([a, b].\)
On montre que la fonction \(f\) est strictement monotone sur \([a, b],\) plus précisément on montre que :
- si \(f(a) < f(b), f\) est strictement croissante sur \([a, b]\)
- si \(f(b) < f(a), f\) est strictement décroissante sur \([a, b].\)
(Ceci se démontrera par un raisonnement identique au précédent en intervertissant les rôles joués par \(f(a)~\textrm{et}~f(b)).\)
On suppose ici que \(a~\textrm{et}~b\) sont des éléments de \(I\) vérifiant \(a < b~\textrm{et}~f(a) < f(b).\)
Soient \(x~\textrm{et}~y, x < y,\) appartenant à \(]a, b[,\) donc en particulier \(a < y < b,\) d'après la première étape, avec \(a\) jouant le rôle de \(u~\textrm{et}~b\) jouant le rôle de \(v,\) \(f(a) < f(b) \Rightarrow f(a) < f(y) < f(b).\)
Alors on a \(f(a) < f(y)~\textrm{et}~x\) appartient à \(]a,y[,\) donc toujours d'après la première étape, \(a\) jouant le rôle de \(u~\textrm{et}~y\) jouant le rôle de \(v,\) on déduit \(f(a) < f(x) < f(y).\)
On a bien montré que si \(f(a) < f(b), \forall (x,y) \in [a, b]^2, x < y \Rightarrow f(x) < f(y).\)
La fonction \(f\) est bien strictement croissante sur \([a, b].\)
On suppose maintenant que \(a~\textrm{et}~b\) sont des éléments de \(I\) vérifiant \(a < b~\textrm{et}~f(b) < f(a).\)
Soient \(x~\textrm{et}~y, x < y,\) appartenant à \(]a, b[,\) donc en particulier \(a < y < b,\) d'après la première étape, \(f(b) < f(a) \Rightarrow f(b) < f(y) < f(a).\)
Alors on a \(f(y) < f(a)~\textrm{et}~x\) appartient à \(]a, y[,\) donc toujours d'après la première étape, on déduit \(f(y) < f(x) < f(a).\)
On a bien montré que si \(f(b) < f(a), \forall (x, y) \in [a, b]^2, x < y \Rightarrow f(y) < f(x).\)
La fonction \(f\) est bien strictement décroissante sur \([a, b].\)
Troisième étape
On montre que la fonction \(f\) est strictement monotone sur \(I.\)
Soient \(a~\textrm{et}~b\) des éléments de \(I\) fixés vérifiant \(a < b.\)
Et soit \(x~\textrm{et}~y\) deux éléments quelconques de \(I, x < y.\)
On introduit les deux éléments de \(I\) suivants : \(c = min(a, x)~\textrm{et}~d = max(b, y).\)
Ces éléments existent puisque \(\mathbb R\) est totalement ordonné, ils dépendent de \(x\) et de \(y.\)
Les réels \(a, b, c, d\) vérifient les inégalités suivantes :
\((i)~~c \leq a < b \leq d\)
\((ii)~~c \leq x < y \leq d\)
Donc \(c\) est strictement inférieur à \(d.\)
D'après la deuxième étape \(f\) est strictement monotone sur \([c, d].\)
Pour déterminer le sens de monotonie, on utilise les inégalités \((i)\) qui prouvent que \(a~\textrm{et}~b\) sont dans l'intervalle \([c, d].\) Donc l'ordre de \(f(a)~\textrm{et}~f(b)\) va imposer le sens de monotonie de \(f\) sur \([c, d].\)
- Si \(f(a) < f(b),\) alors \(f\) est strictement croissante sur \([c, d].\)
- si \(f(b) < f(a),\) alors \(f\) est strictement décroissante sur \([c, d].\)
Pour conclure on utilise les inégalités \((ii)\) qui prouvent que \(x~\textrm{et}~y\) appartiennent à \([c, d].\)
- Donc si \(f(a) < f(b), \forall (x, y) \in I^2 f(x) < f(y).\)
La fonction \(f\) est alors strictement croissante sur \(I.\)
- Et si \(f(b) < f(a), \forall (x, y) \in I^2 f(y) < f(x)\)
La fonction \(f\) est alors strictement décroissante sur \(I.\)
Remarque :
L'hypothèse de la continuité de \(f\) n'intervient pas dans la démonstration de "\(f\) strictement monotone \(\Rightarrow f \)est injective"
Une fonction strictement monotone est toujours injective, qu'elle soit continue ou non ; par contre il est essentiel de supposer que \(f\) est continue sur un intervalle pour démontrer la deuxième partie de la proposition : si on enlève la contrainte de la continuité de la fonction, on peut trouver des fonctions injectives et non monotones.
Exemple : Fonctions injectives et non monotones
On peut trouver des fonctions injectives et non monotones :
1) Soit \(f\) la fonction numérique définie sur l'intervalle \([0, 2]\) par
\(f(x) = \begin{cases} x~~ si~~x \in [0,1[ \\ 3-x~~si~~x \in [1, 2] \end{cases}\)
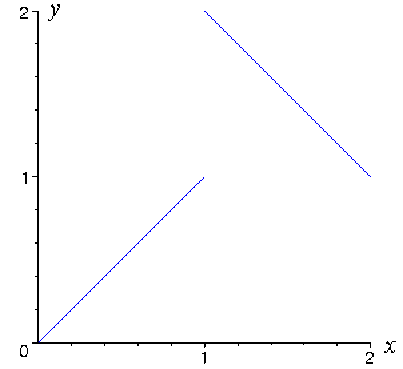
La fonction \(f\) n'est pas continue sur \([0, 2]\): en effet \(f\) n'est pas continue en \(1~~(\displaystyle \lim_{x\rightarrow1^-} f(x)\neq f(1).\)
La fonction \(f\) est injective sur l'intervalle \([0, 2]\)et pourtant elle n'est pas strictement monotone sur \([0, 2].\)
(Par contre sa restriction à l'intervalle \([0,1[\)est strictement monotone mais elle y est aussi continue ; de même sa restriction à l'intervalle \([1, 2]\)).
2) Soit \(g\) la fonction numérique définie sur l'intervalle \([0, 1]\)par \(g(0) = 1, g(1) = 0,~\textrm{et}~\forall x \in ]0,1[~~g(x) = x\)
La fonction \(g\) est injective sur l'intervalle \([0, 1]\)mais n'est pas strictement monotone sur \([0, 1]\); là aussi \(g\) n'est pas continue sur \([0, 1]\)(discontinuité en \(0\) et en \(1\)).