Matrices carrées

Soit \(n\) un entier supérieur ou égal à \(2\). Soient deux entiers distincts \(i\) et\( j\), compris entre\( 1\) et \(n\), et \(\lambda\) un élément de \(\mathbf K\).

1. On définit la matrice \(\mathcal T_{i,j}(\lambda)\in\mathcal M_n(\mathbf K)\) par :

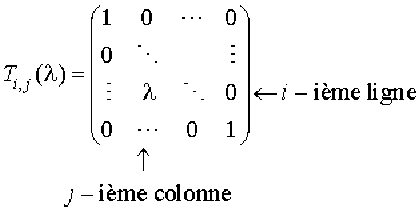
Les éléments de la diagonale principale sont tous égaux à \(1\), le scalaire \( \lambda\) se trouve à la i-ième ligne et j-ième colonne et tous les autres éléments sont nuls.

2. Soit \(\lambda\) un élément non nul de \(\mathbf K\). On définit la matrice diagonale \(\mathcal D_i(\lambda)\in\mathcal M_n(\mathbf K)\) par :

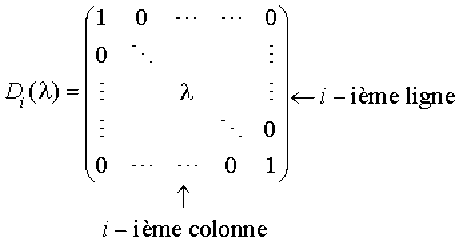
Le scalaire\( \lambda\) se trouve à la i-ième ligne et i-ième colonne, tous les autres éléments de la diagonale principale sont égaux à \(1\).

Les matrices \(\mathcal T_{i,j}(\lambda)\) et \(\mathcal D_i(\lambda)\) sont appelées matrices élémentaires : les matrices \(\mathcal T_{i,j}(\lambda)\) sont dites matrices de transvection et les matrices matrices de dilatation.