Représentations graphiques des solutions d'un système de dimension 2
Une solution d'un système de deux équations
\(\displaystyle{\left\{\begin{array}{ll}x' = f(t,x,y) \\ y' = g(t,x,y)\end{array}\right.}\)
est un couple de fonctions \((u(t), v(t))\), c'est-à-dire une application de \(R\) dans \(R^2\).
Pour en dessiner le graphe, plusieurs options sont possibles.
Méthode : Première représentation
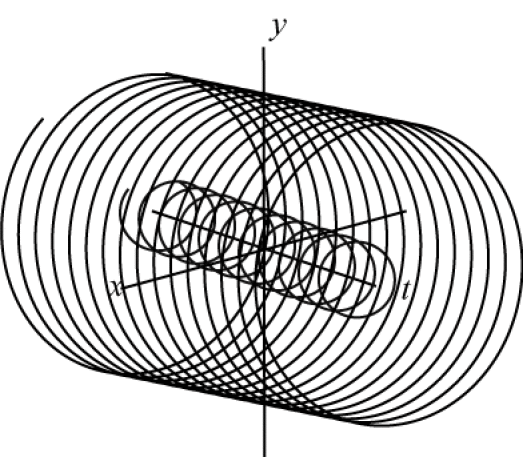
On peut faire un dessin représentant en perspective le graphe de la fonction \(X(t)=(u(t), v(t))\) dans l'espace \(R^3\) des triplets \((t,x,y)\).
Par exemple, les solutions de
\(\displaystyle{\left\{\begin{array}{ll}x'=y \\ y'=-x\end{array}\right.}\)
qui sont de la forme \(x = A \textrm{cos}(t) + B \textrm{sin}(t), y = - A \textrm{sin}(t) + B \textrm{cos}(t)\), sont représentées comme des hélices circulaires :
Méthode : Deuxième représentation
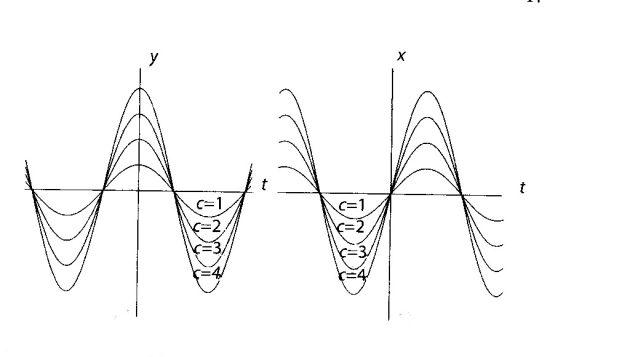
On peut dessiner côte à côte les graphes plans des courbes \(x = u(t), y = v(t)\). Ainsi les solutions de \(x' = y, y' = -x\) sont des sinusoïdes décalées de \(\frac{\pi}{2}\)
La solution vérifiant \(x(0) = 0, y(0) = c\) s'écrit
\(\displaystyle{\left\{\begin{array}{ll}x(t)=c\textrm{sin}t \\ y(t)=c\textrm{cos}t\end{array}\right.}\)
En voici représentées pour quelques valeurs de \(c\).
Méthode : Troisième représentation
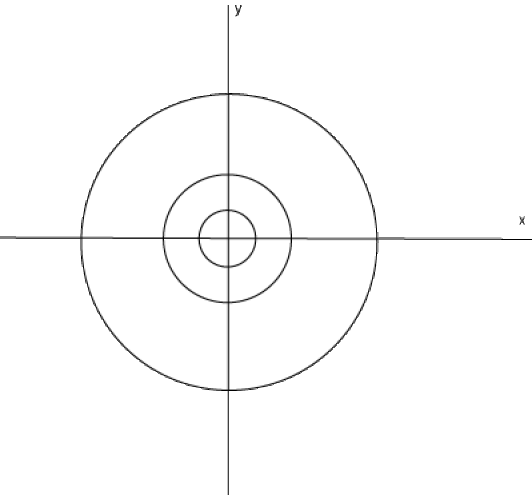
On peut dessiner, dans le plan \((x, y)\), la courbe d'équations paramétriques \(x = u(t), y = v(t)\). En d'autres termes, on dessine l'image dans le plan de la solution \((u(t),v(t))\). Une telle courbe s'appelle une trajectoire[1] du système. Les valeurs de \(t\) n'apparaissent alors pas sur le dessin.
Les trajectoires solutions de \(\displaystyle{\left\{\begin{array}{ll}x'=y \\ y'=-x\end{array}\right.}\) sont des cercles.
Nous verrons que cette représentation est particulièrement adaptée au cas où le système est autonome[2], c'est-à-dire quand il ne dépend pas explicitement de t. C'est bien le cas du système
\(\displaystyle{\left\{\begin{array}{ll}x'=y \\ y'=-x\end{array}\right.}\)